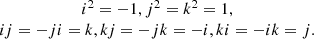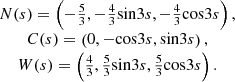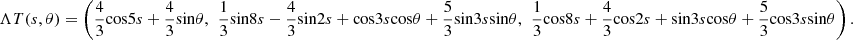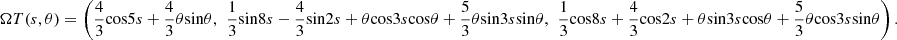| Issue |
4open
Volume 2, 2019
Advances in Researches of Quaternion Algebras
|
|
|---|---|---|
| Article Number | 22 | |
| Number of page(s) | 9 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2019019 | |
| Published online | 05 July 2019 | |
Review Article
On quaternion applications in obtaining surfaces
Department of Mathematics, Faculty of Science, Ankara University, Tandoğan, 06100 Ankara, Turkey
* Corresponding author: yayli@science.ankara.edu.tr
Received:
2
January
2019
Accepted:
21
May
2019
In this paper, we survey the historical development of quaternions and give some recently studies and applications of quaternions of obtaining surfaces.
Mathematics Subject Classification: 11R52 / 14Q05 / 14Q10 / 15B33 / 16H05
Key words: Quaternion algebras / Surfaces / Curves
© Ö. Keskin & Y. Yaylı, Published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Quaternions were advertised by Irish mathematician Sir William Rowan Hamilton in 1843. While he was searching for methods of extensioning complex numbers to higher dimensional spaces, he accidentally invented quaternions. He fell down to find a handy method in three-dimensional space. That is, he could not reach a real in three dimensional skew field. But, he composed quaternions by working in four dimensional space. As to Hamilton, while he was walking with wife over the Royal Canal in Dublin on 16 October 1843, he was experience an epiphany the solution of the equation,
Then, without wasting any time, Hamilton carved this equation with the help of his pocketknife the around the corner Broom Bridge (where Hamilton called Brougham Bridge). The phenomenon is called exploration of the quaternion group. Also, in one sense, Hamilton fathered the cross products and dot products of vector algebra. Moreover, Hamilton characterized a quaternion as a serried four item multiple of real numbers, and identified the first item as the “scalar” part, and the remaining three as the “vector” part [1–3].
Nowadays, the quaternions which are chiefly utilized in computer graphics, control theory and signal processing for representing rotations and orientations are widespread utilized for spacecraft attitude control systems to be commanded. Also, they are utilized to telemeter their current attitude. The logic is that joining quaternion transitions is much more computationally determined then joining a lot of matrix transitions. Quaternions do not possess a computational singularity (unspecified partition by zero) in control and modelling applications that can take place for quarter spin turns (90°) that are accomplishable by several Air, Sea and Space transports. In pure mathematics, quaternions which are one of the four finite dimensional normed division algebras over the real numbers come to light considerably applications from beginning to end algebra and geometry. Also, quaternions are used not only in rotation but also in reflection [4–8].
Let us now examine the works on applications of quaternions in obtaining surfaces. Primarily, the sum, product, point product, division of two quaternions, inverse of a quaternion and its modulus have been defined. In addition, quaternions are represented by the matrix. Also, quaternions are used in rotation. For example, a counterclockwise rotation through an angle α about an axis  can be represented (Fig. 1),
can be represented (Fig. 1),
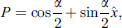 where
where 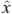 is a unit vector [8].
is a unit vector [8].
 |
Figure 1 A counterclockwise rotation through an angle α about an axis |
If we consider the linear map:
 where
where  ,
, 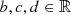 is a unit vector quaternion. That is to say, this expression is called reflection (Fig. 2).
is a unit vector quaternion. That is to say, this expression is called reflection (Fig. 2).
 |
Figure 2 Reflection. |
On the other hand, give the following reference [9] to Definition 1 and Definition 2:
Definition 1
A dual number A has the form A = a + εa* where a and a* are real numbers and ε is the dual symbol subjected to the rules
 A dual quaternion Q is written as
A dual quaternion Q is written as
Hamiltonian conjugate of Q, norm of Q, reciprocal of Q and unit dual quaternion are obtained. Also, screw operators are defined using this dual quaternion.
Definition 2
Let
 and
and
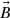 be unit dual vectors in 𝕀𝔻3 (i.e. set of unit vector dual quaternions) the quaternion product of these two dual vectors is given by
be unit dual vectors in 𝕀𝔻3 (i.e. set of unit vector dual quaternions) the quaternion product of these two dual vectors is given by
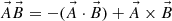 (1)
The expression
(1)
can rewrite as:
(1)
The expression
(1)
can rewrite as:
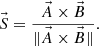 This expression is called
screw operator
(Fig. 3).
This expression is called
screw operator
(Fig. 3).
 |
Figure 3 Screw operator. |
Let’s approach today. In computer graphics, spherical linear interpolation (slerp) is shorth and for spherical linear interpolation, in the context of quaternion interpolation for the purpose of animating 3D rotation [10]. Linear interpolation have been done on Euclidean sphere using quaternions. Also, split-quaternions are elements of a four-dimensional associative algebra introduced by James Cockle in 1849.
Definition 3
A split quaternion q is an expression of the form
 where q
1
, q
2
, q
3
and q
4
are real numbers and i, j, k are split quaternion units which satisfy the non-commutative multiplication rules [11]
where q
1
, q
2
, q
3
and q
4
are real numbers and i, j, k are split quaternion units which satisfy the non-commutative multiplication rules [11]
The linear interpolation on Loretzian sphere Minkowski space have been done using split quaternions. That also yields the shortest possible interpolation path between the two split quaternion on the unit Lorentzian sphere [12].
Spherical spline quaternion interpolation has been done on sphere in Euclidean space using quaternions (Fig. 4). The spline split quaternion interpolation on hyperbolic sphere in Minkowski space has been done using split quaternions and metric Lorentz. This interpolation curve is called spherical spline split quaternion interpolation in Minkowski space (MSquad) (Fig. 5) [13].
 |
Figure 4 The shapes of interpolation are simulated with MATLAB R2010a: (a) Quaternion interpolation between the two key frames in Euclidean space, there are 50 interpolated frames, (b) velocity graph quaternion interpolation [12]. |
 |
Figure 5 The shapes of interpolation are simulated with MATLAB Programming Language. (a) The interpolation curve between two split quaternion on hyperbolic sphere in Minkowski space, there are 50 interpolated frames, (b) inside scope, (c) outside scope, (d) inside scope [13]. |
Quaternions are more usable than three Euler angles in the three dimensional Euclidean space. Thus, many laws in different fields can be given by the quaternions. Canal surfaces and tube surfaces can be obtained by the quaternion product and by the matrix representation. Also, the equation of canal surface given by the different frames of its spine curve can be obtained by the same unit quaternion. In addition, these surfaces are obtained by the homothetic motion [14]. For example, for unit speed curve:
 the Frenet frame vectors can be given as,
the Frenet frame vectors can be given as,
The tube surface X(t, θ) can be obtained by the homothetic motion as X(t, θ) = α(t) + rMN(t), where M is the matrix representation for the unit quaternion q(t, θ) = cosθ + sinθT(t). Moreover, the graphic is as follows (Fig. 6).
All constant slope surfaces are found in the Euclidean 3-space. Namely, those surfaces for which the position vector of a point of the surface makes constant angle with the normal at the surface in that point. These surfaces could be thought as then bi-dimensional analogue of the generalized helices (Fig. 7) [15].
Example 1
Let us point more attention to this picture (but not necessary with
 , when f(v) = (cosv, sinv, 0)). Then,
, when f(v) = (cosv, sinv, 0)). Then,
 for all v and consequently the slope surface is parametrized by
for all v and consequently the slope surface is parametrized by
Circular surfaces are smooth one-parameter families of circles. Three main purposes about circular surfaces and roller coaster surfaces are defined as circular surfaces whose generating circles are lines of curvature. The first one is to reconstruct equations of spacelike circular surfaces and spacelike roller coaster surfaces by using unit split quaternions and homothetic motions.
The second one is to parametrize timelike circular surfaces and give some geometric properties such as striction curves, singularities, Gaussian and mean curvatures. Furthermore, the conditions for timelike roller coaster surfaces to be flat or minimal surfaces are obtained. The last one is to express split quaternionic and matrix representations of timelike circular surfaces and timelike roller coaster surfaces [16].
Example 2
Given a curve
 it is easy to show that
it is easy to show that
 where s is the arc-length parameter of a
1
(s) = e. Using the timelike unit split quaternion q
e
= cosθ + esinθ, we have
where s is the arc-length parameter of a
1
(s) = e. Using the timelike unit split quaternion q
e
= cosθ + esinθ, we have
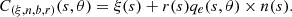 For r = 1 and
For r = 1 and
 , the spacelike circular surfaces are illustrated (Fig. 8).
, the spacelike circular surfaces are illustrated (Fig. 8).
 |
Figure 8 The spacelike circular surfaces with r = 1 and |
Canal surfaces determined by spherical indicatrices of any spatial curve in Minkowski 3-space by means of timelike split quaternions. Moreover, using orthogonal matrices corresponding to these quaternions, the canal surfaces are obtained as homothetic motions. Then, we investigate a relationship between the canal surfaces and unit split quaternions [17].
Example 3
Given a unit-speed spacelike curve
 with spacelike binormal vector, the alternative moving frame vectors are given by
with spacelike binormal vector, the alternative moving frame vectors are given by
Then, the tangent, principal normal and binormal indicatrices of the curve α are obtained as follows:
For the unit timelike split quaternion q N (s, θ) = coshθ + Nsinhθ with timelike vector part, the parametric equation of the canal surface P T (s, θ) constructed by the tangent indicatrix T of the curve α with the admission r(s) = sins is found as follows (Fig. 9);
Then, taking r = 1 and r = θ, respectively, the equations of the tubular and generalized tubular surfaces
 and ΩT(s, θ) generated by the tangent indicatrix T are given by (Fig. 10)
and ΩT(s, θ) generated by the tangent indicatrix T are given by (Fig. 10)
 |
Figure 10 (A). The tubular surface |
Conclusion
In this paper, the historical development of quaternions is surveyed. Also, some recently studies and applications of quaternions of obtaining surfaces are considered. Within the framework of the knowledge acquired, it is observed that applies to many areas of quaternions. The number of these studies is increasing day by day. We were only able to give a small summary. We are very happy to try to contribute to these studies. Our work in this direction continues.
Acknowledgments
The first author would like to thank Tubitak-Bidep for their financial supports during her PhD studies.
References
- Baker Lawrence W (2002), Math and mathematicians series math and mathematicians: the history of math discoveries around the world, UXL, Detroit, MI, p. 207, ISBN 0787638137. [Google Scholar]
- Do Carmo MP (1976), Differential geometry of curves and surfaces, Prentice Hall, Englewood Cliffs, NJ. [Google Scholar]
- Lewis Albert (2004), “Hamilton, William Rowan (1805–1865)”. Oxford Dictionary of National Biography (online ed.). Oxford University Press. doi: 10.1093/ref:odnb/12148, https://en.wikipedia.org/wiki/WilliamRowanHamilton. [Google Scholar]
- Bekar M, Yaylı Y (2013), Involutions of complexified quaternions and split quaternions. Adv Appl Clifford Alg 23, 2, 283–299. [CrossRef] [Google Scholar]
- Bekar M, Yaylı Y (2016), Involution matrices of real quaternions. Caspian J Math Sci 5, 1, 7–16. [Google Scholar]
- Kyrchei II (2012), The theory of the column and row determinants in a quaternion linear algebra, in: AR Baswell (Eds.), Advances in Mathematics Research 15, Nova Sci. Publ, New York, pp. 301–359. [Google Scholar]
- Griffin S (Ed.) (2017), Quaternions: theory and applications, Nova Sci. Publ., New York. ISBN 978-1-53610-768-5. [Google Scholar]
- Zhang F (1997), Quaternions and matrices of quaternions. Linear Alg Appl 251, 21–57. [CrossRef] [Google Scholar]
- Bekar M, Yaylı Y (2013), Dual quaternion involutions and anti-involutions. Adv Appl Clifford Alg 23, 3, 577–592. [CrossRef] [Google Scholar]
- Shoemake K (1985), Animating rotation with quaternion curves. ACM Siggraph 19, 3, 245–254. [Google Scholar]
- Inoguchi J (1998), Timelike surfaces of constant mean curvature in Minkowski 3-space. Tokyo J Math 21, 1, 140–152. [CrossRef] [Google Scholar]
- Ghadami R, Rahebi J, Yaylı Y (2012), Linear interpolation in Minkowski space. Int J Pure Appl Math 77, 4, 469–484. [Google Scholar]
- Ghadami R, Rahebi J, Yaylı Y (2013), Spline split quaternion interpolation in Minkowski space. Adv Appl Clifford Alg 23, 4, 849–862. [CrossRef] [Google Scholar]
- Aslan S, Yaylı Y (2016), Canal surfaces with quaternions. Adv Appl Clifford Alg 26, 31–38. [CrossRef] [Google Scholar]
- Munteanu MI (2010), From golden spirals to constant slope surfaces. AIP J Math Phys 51, 7, 9. [Google Scholar]
- Tuncer OO, Çanakc Z, Gök I, Yaylı Y (2018), Circular surfaces with split quaternionic representations in Minkowski 3-space. Adv Appl Clifford Alg, 28–63, published online June 20, 2018, https://doi.org/10.1007/s00006-018-0883-6. [Google Scholar]
- Kocakusakl E, Tuncer OO, Gök I, Yaylı Y (2017), A new representation of canal surfaces with split quaternions in Minkowski 3-space. Adv Appl Clifford Alg 27, 1387–1409. [CrossRef] [Google Scholar]
Cite this article as: Keskin Ö & Yaylı Y 2019. On quaternion applications in obtaining surfaces. 4open, 2, 22.
All Figures
 |
Figure 1 A counterclockwise rotation through an angle α about an axis |
| In the text | |
 |
Figure 2 Reflection. |
| In the text | |
 |
Figure 3 Screw operator. |
| In the text | |
 |
Figure 4 The shapes of interpolation are simulated with MATLAB R2010a: (a) Quaternion interpolation between the two key frames in Euclidean space, there are 50 interpolated frames, (b) velocity graph quaternion interpolation [12]. |
| In the text | |
 |
Figure 5 The shapes of interpolation are simulated with MATLAB Programming Language. (a) The interpolation curve between two split quaternion on hyperbolic sphere in Minkowski space, there are 50 interpolated frames, (b) inside scope, (c) outside scope, (d) inside scope [13]. |
| In the text | |
 |
Figure 6 Tube surface X(t, θ) [14]. |
| In the text | |
 |
Figure 7 For |
| In the text | |
 |
Figure 8 The spacelike circular surfaces with r = 1 and |
| In the text | |
 |
Figure 9 The canal surface P T (s, θ) constructed by the tangent indicatrix T of α [17]. |
| In the text | |
 |
Figure 10 (A). The tubular surface |
| In the text | |