| Issue |
4open
Volume 3, 2020
|
|
|---|---|---|
| Article Number | 2 | |
| Number of page(s) | 19 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2020001 | |
| Published online | 27 April 2020 | |
Review Article
A survey on pseudo-Chebyshev functions
International Telematic University UniNettuno, Corso Vittorio Emanuele II, 39, 00186 Roma, Italy
* Corresponding author: paoloemilioricci@gmail.com
Received:
9
January
2020
Accepted:
11
February
2020
In recent articles, by using as a starting point the Grandi (Rhodonea) curves, sets of irrational functions, extending to the fractional degree the 1st, 2nd, 3rd and 4th kind Chebyshev polynomials have been introduced. Therefore, the resulting mathematical objects are called pseudo-Chebyshev functions. In this survey, the results obtained in the above articles are presented in a compact way, in order to make the topic accessible to a wider audience. Applications in the fields of weighted best approximation, roots of 2 × 2 non-singular matrices and Fourier series are derived.
Key words: Grandi curves / Pseudo-Chebyshev functions / Recurrence relations / Differential equations / Orthogonality properties
© P.E. Ricci, Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
In preceding articles, starting from Bernoulli’s spiral, in the complex form, we have highlithed the obvious connection between the first and second kind Chebyshev polynomials, and the Grandi (Rodhonea) curves.
As these curves exist even for rational index values, we have extended these Chebyshev polynomials to the case of fractional degree [1]. The resulting functions are no more polynomials, but irrational functions that have been called pseudo-Chebyshev functions, because they satisfy many properties of the corresponding Chebyshev polynomials. Actually the irrationality of these functions is due to a constant factor which is multiplied by polynomials.
In subsequent articles [2, 3], recalling the third and fourth kind Chebyshev polynomials, and their connections to the preceding ones, as it is presented in [4], we have also introduced, for completeness, the corresponding pseudo-Chebyshev functions of the third and fourth kind. It has been shown that these families of functions satisfy the recursion and differential equations of the classical Chebyshev polynomials up to the change of the degree (from the integer to the fractional one). The particular case which seems to be the most important one, is when the degree is of the type k + 1/2, that is a half-integer, since in this case, the pseudo-Chebyshev functions satisfy even the orthogonality properties, in the interval (−1, 1), with respect to the same weights of the classical polynomials.
Archimedes vs. Bernoulli spiral
Spirals are described by polar equations and, in a recent work [1], has been highlithed the connection of the Bernoulli spiral, in complex form, with the Grandi (Rhodonea) curves and the Chebyshev polynomials.
The Archimedes spiral [5] (Fig. 1) has the polar equation: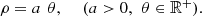 (1)
(1)
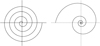 |
Figure 1 Archimedes vs. Bernoulli spiral. |
If θ > 0 the spiral turns counter-clockwise, if θ < 0 the spiral turns clockwise. Bernoulli’s (logarithmic) spiral [6] (Fig. 1) has the polar equation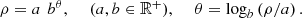 (2)
(2)
By changing the parameters a and b one gets different types of spirals.
The size of the spiral is determined by a, while the verse of rotation and how it is “narrow” depend on b.
Being a and b positive costants, there are some interesting cases. The most popular logarithmic spiral is the harmonic spiral, also called Fibonacci spiral, in which the distance between the spires is in harmonic progression, with ratio 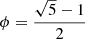 , that is, the “Golden ratio”.
, that is, the “Golden ratio”.
The logarithmic spiral was discovered by René Descartes in 1638, and studied by Jakob Bernoulli (1654–1705).
It is a first example of a fractal. On J. Bernoulli’s tomb there is the sentence: Eadem Mutata Resurgo.
In what follows, we consider a “canonical form” of the Bernoulli spirals assuming a = 1, b = en, that is the simplified polar equation: (3)
(3)
The complex Bernoulli spiral
In the complex case, putting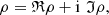 (4)and considering the Bernoulli spiral:
(4)and considering the Bernoulli spiral: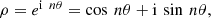 (5)we find:
(5)we find: (6)
(6)
Recalling Chebyshev polynomials
Starting from the equations: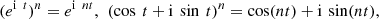 (7)separating the real from the imaginary part, and putting x = cos t, the first and second kind Chebyshev polynomials are derived:
(7)separating the real from the imaginary part, and putting x = cos t, the first and second kind Chebyshev polynomials are derived:![$$ {T}_n(x)\enspace \mathbf{:=} \mathrm{cos}(n\enspace \mathrm{arccos}x)=\sum_{h=0}^{\left[\frac{n}{2}\right]} (-1{)}^h\left(\begin{array}{c}n\\ 2h\end{array}\right){x}^{n-2h}(1-{x}^2{)}^h, $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq10.gif) (8)
(8)![$$ {U}_{n-1}(x)\enspace \mathbf{:=} \frac{\mathrm{sin}(n\enspace \mathrm{arccos}x)}{\mathrm{sin}(\mathrm{arccos}x)}=\sum_{h=0}^{\left[\frac{n-1}{2}\right]} \enspace (-1{)}^h\left(\begin{array}{c}n\\ 2h+1\end{array}\right){x}^{n-2h-1}(1-{x}^2{)}^h. $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq11.gif) (9)
(9)
It is well known that the first kind Chebyshev polynomials [7] play an important role in Approximation theory, since their zeros constitute the nodes of optimal interpolation, because their choice minimizes the error of interpolation. They’re also the optimal nodes for the Gaussian quadrature rules.
The second kind Chebyshev polynomials can be used for representing the powers of a 2 × 2 non singular matrix [8]. Extension of this polynomial falmily to the multivariate case has been considered for the powers of a r × r (r ≥ 3) non singular matrix (see [9, 10]).
Remark 1
Chebyshev polynomials are a particular case of the Jacobi polynomials  [11], which are orthogonal in the interval [−1, 1] with respect to the weight
[11], which are orthogonal in the interval [−1, 1] with respect to the weight 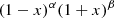 . More precisely, the following equations hold:
. More precisely, the following equations hold: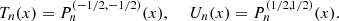 Therefore, properties of the Chebyshev polynomials could be deduced in the framework of hypergeometric functions. However, in this more general approach, the connection with trigonomeric functions disappears.
Therefore, properties of the Chebyshev polynomials could be deduced in the framework of hypergeometric functions. However, in this more general approach, the connection with trigonomeric functions disappears.
Remark 2
In connection with interpolation and quadrature problems, two other types of Chebyshev polynomials have been considered. They correspond to different choices of weights:
These were called by Gautschi [12] the third and fourth kind Chebyshev polynomials, and have been used in Numerical Analysis, mainly in the framework of quadrature rules.
Basic properties of the Chebyshev polynomials of third and fourth kind
The third and fourth kind Chebyshev polynomials have been used by many scholars (see e.g. [4, 13]), because they are useful in particular quadrature rules, when singularities of the integrating function occur only at one end of the considered interval, that is (+1 or −1) (see [14, 15]). They have been shown even to be useful for solving high odd-order boundary value problems with homogeneous or nonhomogeneous boundary conditions [13].
The third and fourth kind Chebyshev polynomials are defined in ![$ [-\mathrm{1,1}]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq16.gif) as follows:
as follows:![$$ \begin{array}{l}{V}_n(x)=\frac{\mathrm{cos}\left[(n+1/2)\mathrm{arccos}x\right]}{\mathrm{cos}[(\mathrm{arccos}x)/2]},\\ \enspace {W}_n(x)=\frac{\mathrm{sin}\left[(n+1/2)\mathrm{arccos}x\right]}{\mathrm{sin}[(\mathrm{arccos}x)/2]}.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq17.gif) (10)
(10)
Since 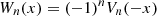 , as it can be see by their graphs (Figs. 2 and 3), the third and fourth kind Chebyshev polynomials are essentially the same polynomial set, but interchanging the ends of the interval
, as it can be see by their graphs (Figs. 2 and 3), the third and fourth kind Chebyshev polynomials are essentially the same polynomial set, but interchanging the ends of the interval ![$ [-\mathrm{1,1}]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq19.gif) .
.
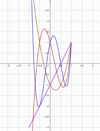 |
Figure 2 Vk (x), k = 1, 2, 3, 4. (1) Violet; (2) brown; (3) red; (4) blue. |
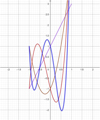 |
Figure 3 Wk (x), k = 1, 2, 3, 4. (1) Violet; (2) brown; (3) red; (4) blue. |
The orthogonality properties hold [4]: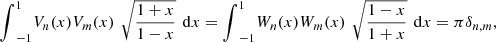 (δ is the Kronecher delta).
(δ is the Kronecher delta).
One of the explicit advantages of Chebyshev polynomials of third and fourth kind is to estimate some definite integrals as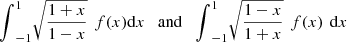 with the precision degree 2n − 1, by using the n interpolatory points
with the precision degree 2n − 1, by using the n interpolatory points 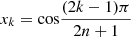 , (k = 1, 2, …, n), in the interval [−1, 1] [13, 14].
, (k = 1, 2, …, n), in the interval [−1, 1] [13, 14].
The Grandi (Rhodonea) curves
The curves with polar equation: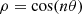 (11)are known as Rhodonea or Grandi curves, in honour of G. Guido Grandi who communicated his discovery to G.W. Leibniz in 1713.
(11)are known as Rhodonea or Grandi curves, in honour of G. Guido Grandi who communicated his discovery to G.W. Leibniz in 1713.
Curves with polar equation: 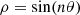 are equivalent to the preceding ones, up to a rotation of
are equivalent to the preceding ones, up to a rotation of 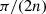 radians.
radians.
The Grandi roses display
n petals, if
 is odd,
is odd,2n petals, if
 is even.
is even.
By using equation (11) it is impossible to obtain, roses with 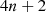 (
( ) petals.
) petals.
Roses with  petals can be obtained by using the Bernoulli Lemniscate and its extensions. More precisely,
petals can be obtained by using the Bernoulli Lemniscate and its extensions. More precisely,
for n = 0, a two petals rose comes from the equation
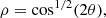 (the Bernoulli Lemniscate),
(the Bernoulli Lemniscate),for n ≥ 1, a 4n + 2 petals rose comes from the equation
![$ \rho ={\mathrm{cos}}^{1/2}[(4n+2)\theta ]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq32.gif) .
.
A few graphs of Rhodonea curves are shown in Figures 4–7.
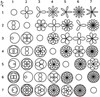 |
Figure 4 Rhodonea |
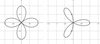 |
Figure 5 Rhodonea cos(2θ) and cos(3θ). |
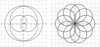 |
Figure 6 Rodoneas |
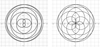 |
Figure 7 Rodoneas |
Pseudo-Chebyshev functions of half-integer degree
In what follows, we consider the case of the half-integer degree, which seems to be the most interesting one, since the resulting pseudo-Chebyshev functions satisfy the orthogonality properties in the interval (−1, 1) with respect to the same weights of the corresponding Chebyshev polynomials.
Definition 1
Note that the above definition holds even for k + 1/2 < 0, taking into account the parity properties of the circular functions.
Recursion for the 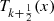 and
and 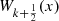
Put for shortness: 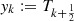 and
and 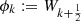 . Then, by using definition (12) and the addition formulas for the sine and cosine functions we find:
. Then, by using definition (12) and the addition formulas for the sine and cosine functions we find: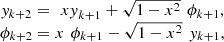 and therefore:
and therefore: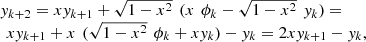 that is the same recursion of the classical Chebyshev polynomials:
that is the same recursion of the classical Chebyshev polynomials: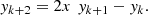 (13)
(13)
Furthermore, the initial conditions for the 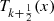 functions are:
functions are: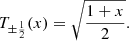 (14)
(14)
Interchanging the roles of 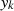 and
and 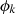 we find that the same recurrence for second sequence holds, but with different initial conditions. We have, precisely:
we find that the same recurrence for second sequence holds, but with different initial conditions. We have, precisely: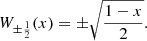 (15)
(15)
Differential equations for the 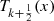 and
and 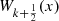
Even the differential equations satified by the  and
and 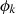 can be recovered by using a coupled technique. In fact, differentating
can be recovered by using a coupled technique. In fact, differentating 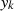 and
and 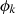 , we find:
, we find: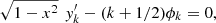
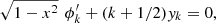 and differentiating again the first equation:
and differentiating again the first equation: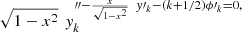 that is:
that is: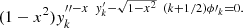
Substituting 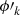 , we find the differential equation satisfied by the
, we find the differential equation satisfied by the 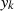 :
: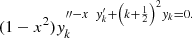 (16)and interchanging the roles of
(16)and interchanging the roles of  and
and 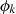 we find that the same differential equation is satisfied by the
we find that the same differential equation is satisfied by the 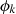 .
.
Remark 3
Remark 4
The case of the 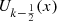 and
and 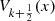
Recalling equation (12), since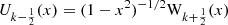 and
and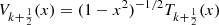 it results that the functions
it results that the functions 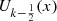 and
and  satisfy the same recursion (13) of the classical Chebyshev polynomials, but with the initial conditions:
satisfy the same recursion (13) of the classical Chebyshev polynomials, but with the initial conditions: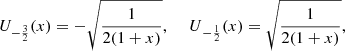 (17)and
(17)and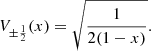 (18)
(18)
Differential equations for the 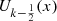 and
and 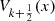
Put for shortness: 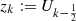 and
and 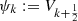 . Differentiating the second equation (12), we find:
. Differentiating the second equation (12), we find: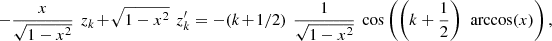 that is
that is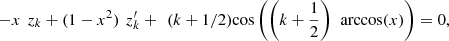 and differentiating again, it results:
and differentiating again, it results: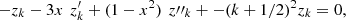 that is
that is![$$ {\begin{array}{ll}(1-{x}^2)\enspace {z}_k^{{\prime\prime}& \end{array}-3x\enspace {z\prime}_k+\left[{\left(k+\frac{1}{2}\right)}^2-1\right]\enspace {z}_k=0. $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq82.gif) (19)and interchanging the roles of
(19)and interchanging the roles of 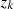 and
and 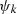 we find that the same differential equation is satisfied by the
we find that the same differential equation is satisfied by the 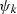 .
.
Remark 5
The first few 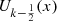 are:
are: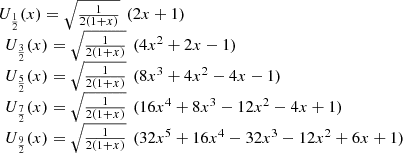 and, in general:
and, in general: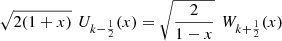
Remark 6
The first few 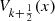 are:
are: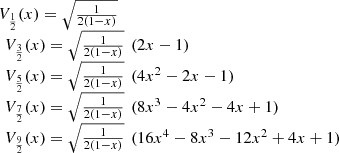 and, in general:
and, in general: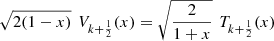
The pseudo-Chebyshev functions 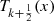 ,
, 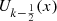 ,
, 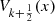 and
and 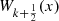 can be represented, in terms of the third and fourth kind Chebyshev polynomials as follows:
can be represented, in terms of the third and fourth kind Chebyshev polynomials as follows: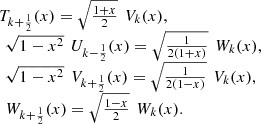 (20)
(20)
In the considered case of half-integer degree, the pseudo-Chebyshev functions satisfy not only the recurrence relations and differential equations analogues to the classical ones, but even the orthogonality properties.
Orthogonality properties of the 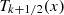 and
and 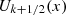 functions
functions
A few graphs of the 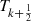 functions are shown in Figure 8.
functions are shown in Figure 8.
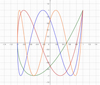 |
Figure 8 Tk+1/2(x), k = 1, 2, 3, 4. (1) Green; (2) red; (3) blue; (4) orange. |
Theorem 1
The pseudo-Chebyshev functions 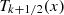 satisfy the orthogonality property:
satisfy the orthogonality property: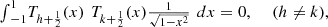 (21)where
(21)where 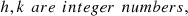
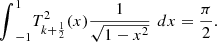 (22)
(22)
A few graphs of the 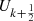 functions are shown in Figure 9.
functions are shown in Figure 9.
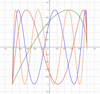 |
Figure 9 Uk+1/2(x), k = 1, 2, 3, 4. (1) Green; (2) red; (3) blue; (4) orange. |
Theorem 2
The pseudo-Chebyshev functions 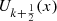 satisfy the orthogonality property:
satisfy the orthogonality property: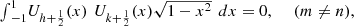 (23)where
(23)where 
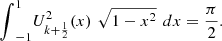 (24)
(24)
Proof. We prove only Theorem 12, since the proof of Theorem 13 is similar.
From the Werner formulas, we have:![$$ \begin{array}{l}{\int }_{-1}^1 \mathrm{cos}\left[\left(h+\frac{1}{2}\right)\mathrm{arccos}(x)\right]\enspace \mathrm{cos}\left[\left(k+\frac{1}{2}\right)\mathrm{arccos}(x)\right]\frac{1}{\sqrt{1-{x}^2}}\enspace \mathrm{d}x=\\ \enspace \end{array}2\enspace {\int }_0^{\pi /2} \mathrm{cos}[(2h+1)t]\mathrm{cos}[(2k+1)t]\enspace \mathrm{d}t=0, $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq109.gif) and
and![$$ \begin{array}{l}{\int }_{-1}^1 {\mathrm{cos}}^2\left[\left(k+\frac{1}{2}\right)\mathrm{arccos}(x)\right]\frac{1}{\sqrt{1-{x}^2}}\enspace {dx}=\enspace 2\enspace {\int }_0^{\frac{\pi }{2}} {\mathrm{cos}}^2\left(\left(2k+1\right)t\right)\mathrm{d}t=\frac{\pi }{2}.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq110.gif) □
□
The third and fourth kind pseudo-Chebyshev functions
The results of this section are based on the excellent survey by Aghigh et al. [4]. By using that article, it is possible to derive, in an almost trivial way, the links among the pseudo-Chebyshev functions and the third and fourth kind Chebyshev polynomials.
We recall here only the principal properties, without proofs. Proofs and other properties are reported in reference [3]. In Figures 10 and 11, we show the graphs of the first few third and fourth kind pseudo-Chebyshev functions.
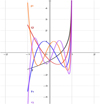 |
Figure 10 Vk+1/2(x), k = 1, 2, 3, 4, 5. (1) Grey; (2) red; (3) blue; (4) orange; (5) violet. |
 |
Figure 11 Wk+1/2(x), k = 1, 2, 3, 4, 5. (1) Red; (2) blue; (3) orange; (4) violet; (5) grey. |
Orthogonality properties of the 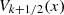 and
and 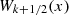 functions
functions
A few graphs of the 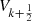 functions are shown in Figure 10.
functions are shown in Figure 10.
Theorem 3
The pseudo-Chebyshev functions 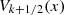 verify the orthogonality property:
verify the orthogonality property: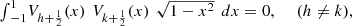 (25)
(25)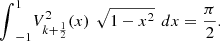 (26)
(26)
A few graphs of the 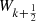 functions are shown in Figure 11.
functions are shown in Figure 11.
Theorem 4
The pseudo-Chebyshev functions 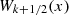 verify the orthogonality property:
verify the orthogonality property: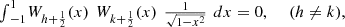 (27)
(27)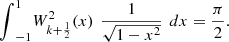 (28)
(28)
Explicit forms
Theorem 5
It is possible to represent explicitly the pseudo-Chebyshev functions as follows:
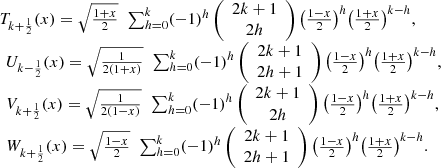 (29)
(29)
Location of zeros
By equation (12), the zeros of the pseudo-Chebyshev functions 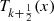 and
and 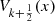 are given by
are given by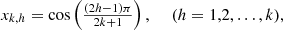 (30)and the zeros of the pseudo-Chebyshev functions
(30)and the zeros of the pseudo-Chebyshev functions 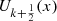 and
and 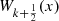 are given by
are given by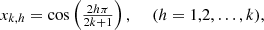 (31)furthermore, the
(31)furthermore, the  functions always vanish at the end of the interval [−1, 1].
functions always vanish at the end of the interval [−1, 1].
Remark 7
More technical properties as the Hypergeometric representations and the Rodrigues-type formulas are reported in [3].
Links with first and second kind Chebyshev polynomials
Theorem 6
The pseudo-Chebyshev functions are connected with the first and second kind Chebyshev polynomials by means of the equations:
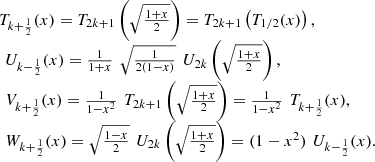 (32)
(32)
Proof. The results follow from the equations: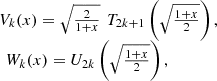 (33)(see [4]), by using definition (12).
(33)(see [4]), by using definition (12).
Remark 8
Note that the first equation, in (29), extends the known nesting property verified by the first kind Chebyshev polynomials: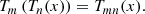 (34)
(34)
This property, already considered in [16] for the first kind pseudo-Chebyshev functions, actually holds in general, as a consequence of the definition Tk(x) = cos(k arccos(x)). Note that this composition identity even holds for the first kind Chebyshev polynomials in several variables [10], as it was proven in [17].
Pseudo-Chebyshev functions with general rational indexes
Basic properties of the pseudo-Chebyshev functions of the first and second kind
We put, by definition: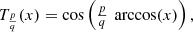 (35)
(35)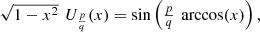 (36)where p and q are integer numbers, (
(36)where p and q are integer numbers, (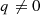 ).
).
Note that definitions (35) and (36) hold even for negative indexes, that is for p/q < 0, according to the parity properties of the trigonometric functions.
The following theorems hold:
Theorem 7
The pseudo-Chebyshev functions 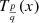 satisfy the recurrence relation
satisfy the recurrence relation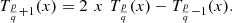 (37)
(37)
Proof. Write equation (37) in the form: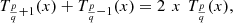 then use definition (35) and the trigonometric identity:
then use definition (35) and the trigonometric identity: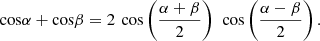
Theorem 8
The first kind pseudo-Chebyshev functions 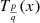 satisfy the differential equation:
satisfy the differential equation: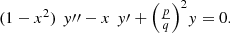 (38)
(38)
so that equation (38) follows.
The following theorems hold:
Theorem 9
The pseudo-Chebyshev functions 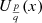 satisfy the recurrence relation
satisfy the recurrence relation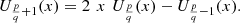 (39)
(39)
Proof. Write equation (39) in the form: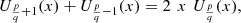 then use definition (36) and the trigonometric identity:
then use definition (36) and the trigonometric identity: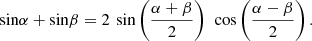
Theorem 10
The pseudo-Chebyshev functions 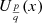 satisfy the differential equation
satisfy the differential equation![$$ \begin{array}{l}(1-{x}^2)\enspace y\mathrm{\prime\prime}-3\enspace x\enspace {y\prime}+\left[{\left(\frac{p}{q}\right)}^2-1\right]\enspace y=0.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq147.gif) (40)
(40)
Proof. Differentiating, and differentiating again equation (36) we find subsequently: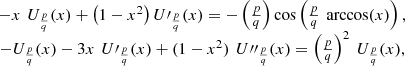 so that equation (40) follows.
so that equation (40) follows.
Basic properties of the pseudo-Chebyshev functions of third and fourth kind
According to equation (10), put by definition:![$$ \begin{array}{l}{V}_{\frac{p}{q}}(x)=\frac{\mathrm{cos}\left[\left(\frac{p}{q}+\frac{1}{2}\right)\mathrm{arccos}x\right]}{\mathrm{cos}[(\mathrm{arccos}x)/2]},\\ \enspace {W}_{\frac{p}{q}}(x)=\frac{\mathrm{sin}\left[\left(\frac{p}{q}+\frac{1}{2}\right)\mathrm{arccos}x\right]}{\mathrm{sin}[(\mathrm{arccos}x)/2]}.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq149.gif) (41)
(41)
Theorem 11
The third and fourth kind pseudo-Chebyshev functions are related to the first and second kind ones by the equations:
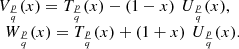 (42)
(42)
Proof. It is sufficient to use the addition formulas for the cosine and sine functions.
Therefore, we can derive the equations: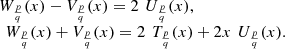 (43)
(43)
Some general formulas
Putting: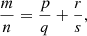 (44)and using the cosine or sine addition formulas, we find:
(44)and using the cosine or sine addition formulas, we find: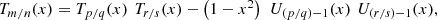 (45)
(45)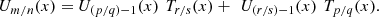 (46)
(46)
Particular results
Combining the above equations, we find: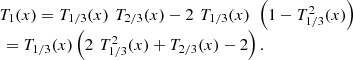 (53)
(53)
Links with the pseudo-Chebyshev functions
The third and fourth kind Chebyshev polynomials are defined as follows:![$$ \begin{array}{l}{V}_n(x)=\frac{\mathrm{cos}\left[(n+1/2)\mathrm{arccos}x\right]}{\mathrm{cos}[(\mathrm{arccos}x)/2]}=\sqrt{\frac{2}{1+x}}\enspace {T}_{n+\frac{1}{2}}(x)={T}_{\frac{1}{2}}^{-1}(x)\enspace {T}_{n+\frac{1}{2}}(x),\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq162.gif) (54)
(54)![$$ \begin{array}{l}{W}_n(x)=\frac{\mathrm{sin}\left[(n+1/2)\mathrm{arccos}x\right]}{\mathrm{sin}[(\mathrm{arccos}x)/2]}=2\enspace \sqrt{\frac{1+x}{2}}\enspace {U}_{n-\frac{1}{2}}(x)=2\enspace {T}_{\frac{1}{2}}(x)\enspace {U}_{n-\frac{1}{2}}(x).\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq163.gif) (55)
(55)
Therefore, we find the equations: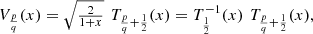 (56)
(56)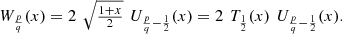 (57)
(57)
Applications
P.L. Chebyshev initiated his 40 years research on approximation with two articles, in connection with the mechanism theory: “Théorie des mécanismes connus sous le nom de parallelélogrammes” (1854) and “Sur les questions de minima qui se rattachent à la représentation approximative des fonctions” (1859) [18]. The origin of these researches is to be found in his desire to improve J. Watt’s steam engine. In fact, the study of a mechanism that converts circular into linear motion, improving the results of Watt, has led him to new problems in approximation theory (the so-called uniform optimal approximation) whose solution makes use of the first kind Chebyshev polynomials.
The problem is posed in these terms:
Assigned a continuous function in ![$ [a,b]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq166.gif) , among all monic polynomials
, among all monic polynomials 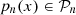 of degree
of degree 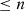 , to find the best uniform approximation, i.e. such that:
, to find the best uniform approximation, i.e. such that:![$$ {E}_n[f]=\underset{{p}_n\in {\mathcal{P}}_n}{\mathrm{inf}}\underset{x\in [a,b]}{\mathrm{max}}|f(x)-{p}_n(x)|=\mathrm{min}. $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq169.gif)
![$ \underset{x\in [a,b]}{\mathrm{max}}|f(x)-{p}_n(x)|=||f(x)-{p}_n(x)|{|}_{\mathrm{\infty }}$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq170.gif) is the uniform norm, (also called minimax norm, or Chebyshev norm). The existence of the minimum was proved by Kirchberger [19] and Borel [20].
is the uniform norm, (also called minimax norm, or Chebyshev norm). The existence of the minimum was proved by Kirchberger [19] and Borel [20].
Assuming, without essential restriction, [a, b] ≡ [−1, 1], and putting f(x) ≡ 0, the solution is given by the first kind (monic) Chebyshev polynomial 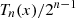 :
: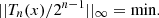
A characteristic property of the best approximation is the “alternating property” (or “equioscillation property”), according to which the best approximation of the zero function attains its maximum absolute value, with alternating signs, at least at  points of the given interval.
points of the given interval.
Weighted minimax approximation by pseudo-Chebyshev functions
In what follows, we deal with a minimax property in [−1, 1] of the type: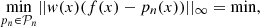 where
where 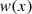 is a weight function. The “alternating property” still characterizes the solution of the problem [15].
is a weight function. The “alternating property” still characterizes the solution of the problem [15].
By nothing that the function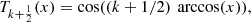 attains its maximum absolute value, with alternating signs, at the points
attains its maximum absolute value, with alternating signs, at the points 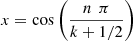 , (n = 0, 1, …, k), it results that
, (n = 0, 1, …, k), it results that
Theorem 12
The minimax approximations to zero on [−1, 1], by monic polynomials of degree n, weighted by 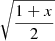 , is given by
, is given by 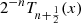 .
.
In a similar way, as the function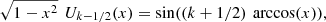 attains its maximum absolute value, with alternating signs, at the points
attains its maximum absolute value, with alternating signs, at the points ![$ x=\mathrm{cos}\left[\frac{n\enspace \pi }{\pm (k+3/2)}\right]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq181.gif) , (n = 0, 1, …, k), it results that
, (n = 0, 1, …, k), it results that
Theorem 13
The minimax approximations to zero on ![$ [-\mathrm{1,1}]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq182.gif) , by monic polynomials of degree n, weighted by
, by monic polynomials of degree n, weighted by 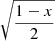 , is given by
, is given by 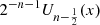 .
.
Roots of a 2 × 2 non-singular complex matrix
The second kind pseudo-Chebyshev functions 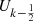 can be used in order to find explicit formulas for the roots of a non-singular 2 × 2 complex matrix.
can be used in order to find explicit formulas for the roots of a non-singular 2 × 2 complex matrix.
Let 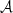 be such a matrix, and denote respectively by
be such a matrix, and denote respectively by 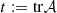 and
and 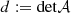 the trace and the determinant of
the trace and the determinant of 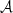 . Then in [8] the second kind Chebyshev polynomials have been used in order to prove the equation:
. Then in [8] the second kind Chebyshev polynomials have been used in order to prove the equation: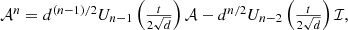 (58)where n is an integer number and
(58)where n is an integer number and 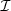 denotes the 2 × 2 identity matrix. Actually this equation still holds when n is replaced by 1/n, in the form:
denotes the 2 × 2 identity matrix. Actually this equation still holds when n is replaced by 1/n, in the form: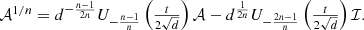 (59)
(59)
Obviously, as the roots in the preceding equation are multi-determined, we have 2n possible values for the n-th root of a 2 × 2 non-singular matrix.
For example, putting n = 2, we find the representation of the square root of 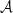 in terms of second kind pseudo-Chebyshev functions:
in terms of second kind pseudo-Chebyshev functions: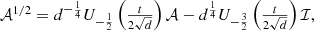 (60)and recalling the initial conditions (17), so that
(60)and recalling the initial conditions (17), so that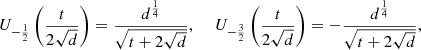 we recover the known equation:
we recover the known equation: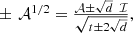 (61)since the roots of d have two (dependent) determinations. Therefore, we find, in total, four possible values for the square root of
(61)since the roots of d have two (dependent) determinations. Therefore, we find, in total, four possible values for the square root of 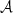 .
.
By using the results in [9] an extension to the roots of a 3 × 3 non-singular complex matrix could be obtained, provided that the matrix eigenvalues are explicitly known. However, the resulting formula is much more involved, and will be reported in another paper.
Representation of the Dirichlet kernel
The Dirichlet kernel 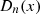 can be expressed in terms of the pseudo-Chebyshev functions.
can be expressed in terms of the pseudo-Chebyshev functions.
Theorem 14
The representation formula of the Dirichlet kernel holds:
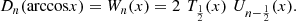 (62)
(62)
Proof. From the well known equation![$$ {D}_n(x)=\frac{\mathrm{sin}[(n+1/2)x]}{\mathrm{sin}(x/2)}, $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq200.gif) it follows:
it follows:![$$ \begin{array}{l}{D}_n(\mathrm{arccos}x)={W}_n(x)=\frac{\mathrm{sin}[(n+1/2)\mathrm{arccos}x]}{\mathrm{sin}[(\mathrm{arccos}x)/2]}=\sqrt{1-{x}^2}\enspace {U}_{n-\frac{1}{2}}(x)\enspace \sqrt{\frac{2}{1-x}}=\sqrt{2\enspace (1+x)}\enspace {U}_{n-\frac{1}{2}}(x)=2\enspace {T}_{\frac{1}{2}}(x)\enspace {U}_{n-\frac{1}{2}}(x).\\ \end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq201.gif)
Summation of trigonometric series
Consider now a trigonometric series of a ![$ {L}^1[-\pi,\pi ]$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq202.gif) ,
, 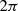 -periodic function f, that is:
-periodic function f, that is: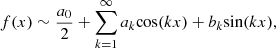 where
where 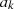 and
and 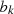 are the Fourier coefficients of
are the Fourier coefficients of 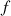 .
.
By Carleson’s theorem [21], the above series converges in mean and even pointwise, up to a set of Lebesgue measure zero.
Writing the partial sums of the above series,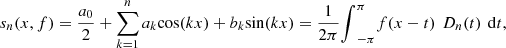 (63)we find the the result:
(63)we find the the result:
Theorem 15
The partial sums of a Fourier series can be represented, in terms of the pseudo-Chebyshev functions, in the form:
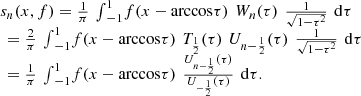 (64)
(64)
Conclusion
The growth of living organisms is often described by the Bernoulli’s logarithmic spiral, which is one of the first examples of fractals. The study of natural forms is commonly associated with mathematical entities like extensions of Lamé’s curves, Grandi’s roses, Bernoulli’s lemniscate, etc.
In this article it has been shown that innumerable plane forms can be described by means of polar equations that extend some of the above mentioned geometrical entities. Moreover, the consideration of Grandi’s roses in the case of fractional indexes gives rise, in a natural way, to mathematical functions that generalize to the case of fractional degree the classical Chebyshev polynomials. The resulting functions, called of pseudo-Chebyshev type, verify many properties of the corresponding polynomials and, in the case of half-integer degree, also the orthogonality properties.
Applications have been shown in the fields of weighted best approximation, roots of 2 × 2 non-singular matrices and Fourier series.
References
- Ricci PE (2018), Complex spirals and pseudo-Chebyshev polynomials of fractional degree. Symmetry 10, 671. [Google Scholar]
- Cesarano C, Ricci PE (2019), Orthogonality properties of the pseudo-Chebyshev functions (variations on a Chebyshev’s theme). Mathematics 7, 180. https://doi.org/10.3390/math7020180. [CrossRef] [Google Scholar]
- Cesarano C, Pinelas S, Ricci PE (2019), The third and fourth kind pseudo-Chebyshev polynomials of half-integer degree. Symmetry 11, 274. https://doi.org/10.3390/sym11020274. [Google Scholar]
- Aghigh K, Masjed-Jamei M, Dehghan M (2008), A survey on third and fourth kind of Chebyshev polynomials and their applications. Appl Math Comput 199, 2–12. [Google Scholar]
- Heath TL (1897), The Works of Archimedes, Cambridge Univ. Press, Google Books. [Google Scholar]
- Archibald RC (1920), Notes on the logarithmic spiral, golden section and the Fibonacci series, in: J. Hambidge (Ed.), Dynamic symmetry, Yale Univ. Press, New Haven, pp. 16–18. [Google Scholar]
- Rivlin TJ (1974), The Chebyshev polynomials, J. Wiley and Sons, New York. [Google Scholar]
- Ricci PE (1974–1975), Alcune osservazioni sulle potenze delle matrici del secondo ordine e sui polinomi di Tchebycheff di seconda specie. Atti Accad Sci Torino 109, 405–410. [Google Scholar]
- Ricci PE (1976), Sulle potenze di una matrice. Rend Mat 9, 179–194. [Google Scholar]
- Ricci PE (1978), I polinomi di Tchebycheff in più variabili. Rend Mat 11, 295–327. [Google Scholar]
- Srivastava HM, Manocha HL (1984), A Treatise on Generating Functions, Halsted Press (Ellis Horwood Limited, Chichester), J. Wiley and Sons, New York, Chichester, Brisbane and Toronto. [Google Scholar]
- Gautschi W (1992), On mean convergence of extended Lagrange interpolation. J Comput Appl Math 43, 19–35. [Google Scholar]
- Doha EH, Abd-Elhameed WM, Alsuyuti M.M. (2015), On using third and fourth kinds Chebyshev polynomials for solving the integrated forms of high odd-order linear boundary value problems. J Egypt Math Soc 23, 397–405. [CrossRef] [Google Scholar]
- Mason JC (1993), Chebyshev polynomials of the second, third and fourth kinds in approximation, indefinite integration, and integral transforms. J Comput Appl Math 49, 169–178. [Google Scholar]
- Mason JC, Handscomb DC (2003), Chebyshev Polynomials, Chapman and Hall, New York, NY, CRC, Boca Raton. [Google Scholar]
- Brandi P, Ricci PE (2019), Some properties of the pseudo-Chebyshev polynomials of half-integer degree. Tbilisi Math J 12, 111–121. [CrossRef] [Google Scholar]
- Ricci PE (1986), Una proprietà iterativa dei polinomi di Chebyshev di prima specie in più variabili. Rend Mat Appl 6, 555–563. [Google Scholar]
- Butzer P, Jongmans F (1999), P.L. Chebyshev (1821–1894). A guide to his life and work. J Approx Theory 96, 111–138. [Google Scholar]
- Kirchberger P (1903), Űber Tschebyscheffsche Annäherungsmethoden (Diss., Gött. 1902). Math. Ann. 57, 509–540. [Google Scholar]
- Borel E (1905), Leçons sur les fonctions de variables réelles et les développements en série de polynomes, Gauthier-Villars, Paris. [Google Scholar]
- Carleson L (1966), On convergence and growth of partial sums of Fourier series. Acta Math 116, 135–157. [CrossRef] [Google Scholar]
All Figures
 |
Figure 1 Archimedes vs. Bernoulli spiral. |
| In the text | |
 |
Figure 2 Vk (x), k = 1, 2, 3, 4. (1) Violet; (2) brown; (3) red; (4) blue. |
| In the text | |
 |
Figure 3 Wk (x), k = 1, 2, 3, 4. (1) Violet; (2) brown; (3) red; (4) blue. |
| In the text | |
 |
Figure 4 Rhodonea |
| In the text | |
 |
Figure 5 Rhodonea cos(2θ) and cos(3θ). |
| In the text | |
 |
Figure 6 Rodoneas |
| In the text | |
 |
Figure 7 Rodoneas |
| In the text | |
 |
Figure 8 Tk+1/2(x), k = 1, 2, 3, 4. (1) Green; (2) red; (3) blue; (4) orange. |
| In the text | |
 |
Figure 9 Uk+1/2(x), k = 1, 2, 3, 4. (1) Green; (2) red; (3) blue; (4) orange. |
| In the text | |
 |
Figure 10 Vk+1/2(x), k = 1, 2, 3, 4, 5. (1) Grey; (2) red; (3) blue; (4) orange; (5) violet. |
| In the text | |
 |
Figure 11 Wk+1/2(x), k = 1, 2, 3, 4, 5. (1) Red; (2) blue; (3) orange; (4) violet; (5) grey. |
| In the text | |


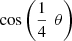
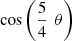
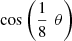
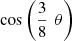
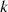
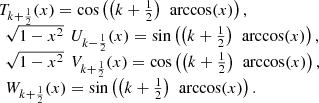
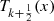
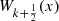
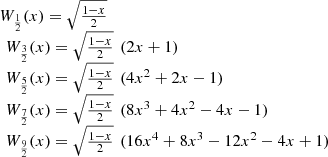
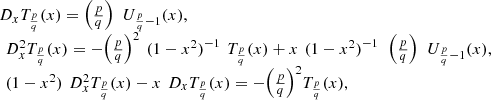
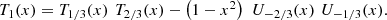
![$$ \begin{array}{l}{T}_1(x)=\mathrm{cos}\left[3\cdot \frac{1}{3}\mathrm{arccos}(x)\right]=4\enspace {T}_{1/3}^3(x)-3\enspace {T}_{1/3}(x).\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq156.gif)
![$$ \begin{array}{l}{T}_2(x)=\mathrm{cos}\left[3\cdot \frac{2}{3}\mathrm{arccos}(x)\right]=4\enspace {T}_{2/3}^3(x)-3\enspace {T}_{2/3}(x).\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq157.gif)
![$$ \begin{array}{l}{T}_{2/3}(x)=\mathrm{cos}\left[2\cdot \frac{1}{3}\mathrm{arccos}(x)\right]=1-2\enspace {\mathrm{sin}}^2\left[\frac{1}{3}\mathrm{arccos}(x)\right]\\ \enspace \hspace{1em}\hspace{1em}\hspace{1em}=1-2\enspace (1-{x}^2)\enspace {U}_{-2/3}(x).\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq158.gif)
![$$ \begin{array}{l}{U}_{-1/3}(x)=\frac{\mathrm{sin}\left[2\cdot \frac{1}{3}\mathrm{arccos}(x)\right]}{\sqrt{1-{x}^2}}\\ \enspace =\frac{2}{\sqrt{1-{x}^2}}\enspace \mathrm{sin}\left[\frac{1}{3}\mathrm{arccos}(x)\right]\enspace \mathrm{cos}\left[\frac{1}{3}\mathrm{arccos}(x)\right]=2\enspace {U}_{-2/3}(x)\enspace {T}_{1/3}(x).\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq159.gif)
![$$ \begin{array}{l}{U}_{-2/3}(x)=\frac{\mathrm{sin}\left[\frac{1}{3}\mathrm{arccos}(x)\right]}{\sqrt{1-{x}^2}}=\sqrt{\frac{1-{T}_{1/3}^2(x)}{1-{x}^2}}.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200001/fopen200001-eq160.gif)