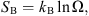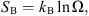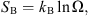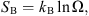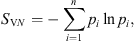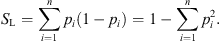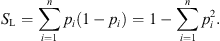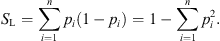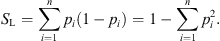| Issue |
4open
Volume 5, 2022
Logical Entropy
|
|
|---|---|---|
| Article Number | E1 | |
| Number of page(s) | 2 | |
| DOI | https://doi.org/10.1051/fopen/2022005 | |
| Published online | 17 March 2022 | |
Editorial
Logical entropy – special issue
Université de Strasbourg, CNRS, Institut de Physique et Chimie des Matériaux de Strasbourg, UMR 7504, 67000 Strasbourg, France
* Corresponding author: giovanni.manfredi@ipcms.unistra.fr
Received:
10
February
2022
Accepted:
10
February
2022
Entropy is a fundamental quantity in many areas of knowledge, from physics to information science to biology. Originally put forward in the nineteenth century for very practical purposes (to quantify the reversibility of thermodynamic cycles, hence of thermal engines), entropy was the key concept that allowed Ludwig Boltzmann to bridge the gap between the (time irreversible) macroscopic thermodynamics and the (reversible) microscopic Newtonian physics. As defined by Boltzmann, the entropy SB represents the number of microscopic states that are compatible with a given macroscopic realization:
where kB is Boltzmann’s constant and Ω is the relevant phase space volume, which is a measure of the number of microscopic states. Note that the logarithm in the above definition is required so that Boltzmann’s statistical entropy possesses the same additive properties as the thermodynamic entropy.
Later, Claude Shannon discovered that a similar formula to Boltzmann’s (albeit with the opposite sign) can be used to quantify the information content of a signal. Following Shannon’s work, it is customary to identify entropy with the (lack of) information or “disorder” of a system. As information is a concept that permeates many natural sciences, the concept of entropy quickly spread to other fields, such as biology and genetics.
It was John von Neumann who generalized the Boltzmann entropy to quantum physics. This is actually more than a mere generalization. Indeed, equation (1) is somewhat problematic, as Ω has the dimensions of a phase space volume, while the argument of the logarithm should be nondimensional – not to mention that SB can become negative. But considering that quantum mechanics introduces a minimal action given by Planck’s constant h, Boltzmann’s formula can be rewritten as: SB = kln(Ω/hd) (where d is the number of dimensions of the system), which is always nonnegative as long as Ω ≥ hd and vanishes only when the equality sign holds. In terms of discrete quantum states with occupation probabilities pi, the von Neumann entropy reads as
which is always positive and only vanishes when one state is occupied with probability equal to one.
While it is generally admitted that the Boltzmann/von Neumann/Shannon entropy is a measure of the lack of information of a system, it is also clear that such a measure is not unique. Given a set of events endowed with probabilities pi, one can construct many other formulae that quantify our uncertainty about the actual observed outcome. And indeed, many other definitions of entropy have been proposed in the past [1], so many that it is virtually impossible to do justice to all of them. In physics, Tsallis’ entropies are a popular example [2], as are Rényi’s entropies [3]. In biology too, several measures of biological diversity have been put forward, see for instance the recent review [4].
How is one to navigate among this plethora of entropy definitions? An answer was provided recently by Ellerman [5], who emphasized the importance of making distinctions between elements of a given set U. If such a set is partitioned into a number n of subsets Bi (such that 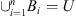 ), each endowed with a probability pi of finding an element of U in that subset, then the probability that in two independent draws one will obtain elements in distinct subsets Bi and
), each endowed with a probability pi of finding an element of U in that subset, then the probability that in two independent draws one will obtain elements in distinct subsets Bi and 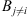 is:
is: 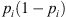 . This is precisely the concept of distinction, i.e., the ability to establish that two independent draws are different from one another. Summing over all n subsets, we obtain the total number of distinctions, which is the definition of what Ellerman termed logical entropy:
. This is precisely the concept of distinction, i.e., the ability to establish that two independent draws are different from one another. Summing over all n subsets, we obtain the total number of distinctions, which is the definition of what Ellerman termed logical entropy:
The subsets Bi may contain one single element, in which case SL represents the probability that two consecutive draws yield different elements of U. SL varies in the interval [0,1], and the lower bound is reached when one element has probability pi = 1, while for all others  . For equal probabilities (
. For equal probabilities (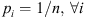 ), one gets:
), one gets:  , when
, when 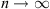 .
.
Although the formula (3) is not itself original (for instance, it is a special case of the Tsalllis entropy), its interpretation in terms of partitions of a set is new and illuminating. Indeed, the logical entropy enjoys a number of intriguing features (e.g., it has the properties of a measure, in the precise mathematical sense) which single it out among the many other definitions proposed in the literature.
This Special Issue contains a collection of four papers devoted to the logical entropy and its applications to physics, particularly quantum mechanics.
The paper by David Ellerman [6] contains an exhaustive introduction, both conceptual and historical, to the logical entropy. In particular, it discusses how the latter relates to the more usual Shannon entropy in quantifying the informational content of a set.
The paper by Boaz Tamir et al. [7] discusses the possible extension of the logical entropy to the quantum domain. Indeed, the logical entropy can be expressed in terms of the density matrix ρ as: 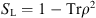 , and quantifies the purity of a quantum state. The authors prove several properties of this entropy for generic density matrices that are relevant to various areas of quantum mechanics and quantum information.
, and quantifies the purity of a quantum state. The authors prove several properties of this entropy for generic density matrices that are relevant to various areas of quantum mechanics and quantum information.
The paper by Denis Sunko [8] addresses the logical entropy in the context of many-body quantum mechanics. It shows how the logical entropy can be used to distinguish many-body fermion states by their information content, although they are pure states whose usual quantum entropies are equal to zero.
Finally, the paper by Giovanni Manfredi [9] points out that the definition of logical entropy (3) lends itself quite naturally to a generalization of probabilities to negative values, an idea that goes back to Feynman and Wigner. By combining negative probabilities with the definition of logical entropy, one can recover many intriguing properties that are typical of quantum systems.
We hope this Special Issue will foster research into a topic that has a long and distinguished past history, but still much potential for future developments.
References
- Wehrl A (1978), General properties of entropy. Rev Mod Phys 50, 221. https://doi.org/10.1103/RevModPhys.50.221. [CrossRef] [Google Scholar]
- Tsallis C (1988), Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys 52, 479. [CrossRef] [Google Scholar]
- Rényi A (1961), On Measures of Entropy and Information, in: J. Neyman (Ed.), Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, University of California Press, pp. 547–561. [Google Scholar]
- Crupi V (2019), Measures of biological diversity: Overview and unified framework. in: E. Casetta, J. Marques da Silva, D. Vecchi (Eds.), From Assessing to Conserving Biodiversity: Conceptual and Practical Challenges, Springer, Cham, pp. 123–136. https://doi.org/10.1007/978-3-030-10991-2_6. [CrossRef] [Google Scholar]
- Ellerman D (2018), Logical entropy: introduction to classical and quantum logical information theory. Entropy 20, 679. https://www.mdpi.com/1099-4300/20/9/679. [CrossRef] [Google Scholar]
- Ellerman D (2022), Introduction to logical entropy and its relationship to Shannon entropy. 4open 5, 1. https://doi.org/10.1051/fopen/2021004. [CrossRef] [EDP Sciences] [Google Scholar]
- Tamir B, De Paiva IL, Schwartzman-Nowik Z, Cohen E (2022), Quantum logical entropy: fundamentals and general properties. 4open 5, 2. https://doi.org/10.1051/fopen/2021005. [CrossRef] [EDP Sciences] [Google Scholar]
- Sunko DK (2022), Entropy of pure states: not all wave functions are born equal. 4open 5, 3. https://doi.org/10.1051/fopen/2021006. [CrossRef] [EDP Sciences] [Google Scholar]
- Manfredi G (2022), Logical entropy and negative probabilities in quantum mechanics. 4open 5, 8. https://doi.org/10.1051/fopen/2022004. [Google Scholar]
Cite this article as: Manfredi G 2022. Logical entropy – special issue. 4open, 5, E1.
© G. Manfredi, Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.