Search
Menu
All issues Volume 3 (2020) 4open, 3 (2020) 7 References
Open Access
Issue
4open
Volume 3, 2020
Article Number 7
Number of page(s) 48
Section Mathematics - Applied Mathematics
DOI https://doi.org/10.1051/fopen/2020007
Published online 31 August 2020
  1. Tavkhelidze I (2001), On the some properties of one class of geometrical figures and lines. Reports of Enlarged Sessions of the Seminar of I. Vekua Institute of Applied Mathematics 16, 1, 35–38. [Google Scholar]
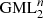  2. Gielis J, Tavkhelidze I, Ricci PE (2013), About “bulky” links generated by generalized Möbius-Listing bodies Formula . J Math Sci 193, 3, 449–460. [CrossRef] [Google Scholar]
  3. Tavkhelidze I (2011), About connection of the generalized Möbius listing’s surfaces with sets of ribbon knots, in: Proceedings of Ukrainian Mathematical Congress S. 2, Topology and geometry – Kiev, pp. 117–129. [Google Scholar]
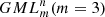  4. Tavkhelidze I, Cassisa C, Gielis J, Ricci PE (2013), About bulky links, generated by generalized Mobius-Listing’s bodies Formula . Rendic Lincei Mat Appl 24, 11–3. [Google Scholar]
  5. Tavkhelidze I, Ricci PE (2017), Some properties of “bulky” links, generated by generalised Möbius–Listing’s bodies, in: Modeling in Mathematics, Atlantis Press, Paris, pp. 159–185. [Google Scholar]
  6. Pinelas S, Tavkhelidze I (2017), Analytic representation of generalized Möbius-listing’s bodies and classification of links appearing after their cut, in: International Conference on Differential & Difference Equations and Applications, Springer, Cham, pp. 477–493. [Google Scholar]
  7. Gielis J (2003), A generic geometric transformation that unifies a wide range of natural and abstract shapes. Am J Bot 90, 3, 333–338. [CrossRef] [PubMed] [Google Scholar]
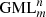  8. Tavkhelidze I, Gielis J (2018), The process of cutting Formula bodies with dm knives, in: Reports of the Enlarged Sessions of the Seminar of I. Vekua Institute of Applied Mathematics Vol. 32. [Google Scholar]
  9. Gielis J, Haesen S, Verstraelen L (2005), Universal shapes: from the supereggs of Piet Hein to the cosmic egg of George Lemaître. Kragujev J Math 28, 55–67. [Google Scholar]
  10. Gielis J (2001), Inventing the Circle, Geniaal, Antwerpen (2003), in: Dutch: De uitvinding van de Cirkel (2001), In Dutch. [Google Scholar]
  11. Gielis J (2017), The Geometrical Beauty of Plants, Atlantis-Springer. [CrossRef] [Google Scholar]
  12. Matsuura M (2015), Gielis’ superformula and regular polygons. J Geom 106, 2, 1–21. [CrossRef] [Google Scholar]
  13. Fougerolle YD, Gribok A, Foufou S, Truchetet F, Abidi MA (2006), Radial supershapes for solid modeling. J Comput Sci Technol 21, 2, 238–243. [Google Scholar]
  14. Gielis J, Natalini P, Ricci PE (2017), A note about generalized forms of the Gielis formula, in: Modeling in Mathematics, Atlantis Press, Paris, pp. 107–116. [Google Scholar]
  15. Abbott EA (1884), Flatland, A Romance of Many Dimensions. By A. Square, Seeley, London. [Google Scholar]
  16. Cutting bamboo poles [Google Scholar]
  17. Haesen S, Šebeković A, Verstraelen L (2003), Relations between intrinsic and extrinsic curvatures. Kragujevac J Math 25, 25, 139–145. [Google Scholar]
  18. Weisstein EW (2009), CRC Encyclopedia of Mathematics, CRC Press, USA. [Google Scholar]
  19. Nisley E (2016), Plotting like it’s 1999 – scrap to Superformula, Poughkeepsie ACM Chapter. [Google Scholar]
  20. Fougerolle Y, Truchetet F, Gielis J (2017), Potential fields of self intersecting Gielis curves for modeling and generalized blending techniques, in: Modeling in Mathematics, Atlantis Press, Paris, pp. 67–81. [Google Scholar]
  21. Shapiro V (2007), Semi-analytic geometry with R-functions. Acta Num 16, 239–303. [CrossRef] [Google Scholar]
  22. Rvachev V (1974), Methods of logic algebra in mathematical physics, Naukova Dumka, Kiev (in Russian). [Google Scholar]
  23. Rvachev VL, Rvachev VA (1979), Neklassicheskie metody teorii priblizhenij v kraevyh zadachah [Non-classical methods of approximation theory to boundary tasks], Naukova dumka Publ, Kiev. [Google Scholar]
  24. Euler L (1965), Leonhard Euler und Christian Goldbach, Briefwechsel 1729–1764, in: A.P. Juskevic, E. Winter (Eds.), , Akademie Verlag, Berlin. [Google Scholar]
  25. Euler L (1758–59), Novi Commentarii Academiae Scientarium Imperialis Petropolitanque 7, pp. 9–28. [Google Scholar]
  26. Lamé G (1838), Un polygone convex étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales? J Math Pure Appl 3, 505–507. [Google Scholar]
  27. Koshy T (2009), Catalan Numbers with Applications, Oxford University Press, New York. [Google Scholar]
  28. Birmajer D, Gil JB, Weiner MD (2017), Colored partitions of a convex polygon by noncrossing diagonals. Discrete Math 340, 4, 563–571. [Google Scholar]
  29. Mallinson PR (1998), Proof without words: Area under a polygonal arch. Math Mag 71, 2, 141–141. [CrossRef] [Google Scholar]
  30. Galilei G (1638), Dialogue concerning the two chief world systems. [Google Scholar]
  31. Cartwright JH, González DL (2016), Möbius strips before Möbius: Topological hints in ancient representations. Math Intell 38, 2, 69–76. [CrossRef] [Google Scholar]
  32. D’Arcy TW (1917), On growth and form, Cambridge University Press. [Google Scholar]
  33. Gielis J, Tavkelidze I, Caratelli D, Fougerolle Y, Ricci PE, Gerats T (2012), Bulky knots and links generated by cutting Generalized Möbius Listing bodies and applications in the natural sciences, in: Royal Academy of Flanders. Proceedings of Math Art Summit 2012, Brussels. [Google Scholar]
  34. Weeks JR (1985), The shape of space. How to visualize surfaces and three-dimensional manifolds, Marcel Dekker. Chapter 17 Bundles. [Google Scholar]
  35. Tavkhelidze I, Caratelli D, Gielis J, Ricci PE, Rogava M, Transirico M (2017), On a geometric model of bodies with “Complex” configuration and some movements, in: Modeling in Mathematics, Atlantis Press, Paris, pp. 129–158. [Google Scholar]
  36. Starostin EL, Van Der Heijden GHM (2007), The shape of a Möbius strip. Nat Mater 6, 8, 563. [CrossRef] [PubMed] [Google Scholar]
  37. Todhunter I (1893), The history of elasticity and of the Strength of Materials – from Galilei to the present time, Volume II Saint-Venant to Lord Kelvin, Part 1, Cambridge University Press. [Google Scholar]
  38. Vekua IN (1985), Shell theory: general methods of construction, Vol. 25, Addison-Wesley Longman. [Google Scholar]