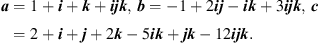Eigenvalues of matrices related to the octonions

Rogério Serôdio; Patricia Beites; José Vitória

doi:10.1051/fopen/2019014

All issues

Volume 2 (2019)

4open, 2 (2019) 16

Full HTML

Advances in Researches of Quaternion Algebras

Open Access

Issue		4open Volume 2, 2019 Advances in Researches of Quaternion Algebras


Article Number		16
Number of page(s)		7
Section		Mathematics - Applied Mathematics
DOI		https://doi.org/10.1051/fopen/2019014
Published online		05 June 2019

4open 2019, 2, 16

Research Article

Eigenvalues of matrices related to the octonions

Rogério Serôdio¹^*, Patricia Beites¹ and José Vitória²

¹ Departamento de Matemática and CMA-UBI, Universidade da Beira Interior, 6201-001 Covilhã, Portugal
² Departamento de Matemática, Universidade de Coimbra, 3004-531 Coimbra, Portugal

^* Corresponding author: rserodio@ubi.pt

Received: 29 December 2018
Accepted: 20 April 2019

Abstract

A pseudo real matrix representation of an octonion, which is based on two real matrix representations of a quaternion, is considered. We study how some operations defined on the octonions change the set of eigenvalues of the matrix obtained if these operations are performed after or before the matrix representation. The established results could be of particular interest to researchers working on estimation algorithms involving such operations.

Mathematics Subject Classification: 11R52 / 15A18

Key words: Octonions / Quaternions / Real matrix representations / Eigenvalues

© R. Serôdio et al., Published by EDP Sciences, 2019

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Due to nonassociativity, the real octonion division algebra is not algebraically isomorphic to a real matrix algebra. Despite this fact, pseudo real matrix representations of an octonion may be introduced, as in [1], through real matrix representations of a quaternion.

In this work, the left matrix representation of an octonion over $R$ $\mathbb{R}$ , as called by Tian in [1], is considered. For the sake of completeness, some definitions and results, in particular on this pseudo representation, are recalled in Section 2.

Using the mentioned representation, results concerning eigenvalues of matrices related to the octonions are established in Section 3. Previous research on this subject, although not explicitly applying real matrix representations of a quaternion, can be seen in [2].

2 Real octonion division algebra

Consider the real octonion division algebra $O$ $\mathbb{O}$ , that is, the usual real vector space $R^{8}$ ${\mathbb{R}}^8$ , with canonical basis ${e_{0}, \dots, e_{7}}$ $\{{e}_0,\dots,{e}_7\}$ , equipped with the multiplication given by the relations

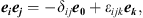$e_{i} e_{j} = - δ_{ij} e_{0} + ε_{ijk} e_{k},$ ${{e}}_{{i}}{{e}}_{{j}}=-{\delta }_{{ij}}{{e}}_{\mathbf{0}}+{\epsilon }_{{ijk}}{{e}}_{{k}},$ where δ _ij is the Kronecker delta, ε _ijk is a Levi-Civita symbol, i.e., a completely antisymmetric tensor with a positive value +1 when ijk = 123, 145, 167, 246, 275, 374, 365 and e ₀ is the identity. This element will be omitted whenever it is clear from the context.

Every element o ∈ $O$ $\mathbb{O}$ can be written as $\begin{matrix} o = \sum_{l = 0}^{7} o_{l} e_{l} = Re (o) + Im (o), & o_{l} \in R, \end{matrix}$ $\begin{array}{cc}{o}=\sum_{\mathcal{l}=0}^7 {o}_{\mathcal{l}}{{e}}_{\mathcal{l}}=\mathrm{Re}\enspace \left({o}\right)+\mathrm{Im}\enspace \left({o}\right),& {o}_{\mathcal{l}}\in R,\end{array}$ where Re( o ) = o ₀ and $Im (o) \equiv \vec{o} = \sum_{l = 1}^{7} o_{l} e_{l}$ $\mathrm{Im}({o})\equiv \overrightarrow{{o}}={\sum }_{\mathcal{l}=1}^7 {o}_{\mathcal{l}}{{e}}_{\mathcal{l}}$ are called the real part and the imaginary (or vector) part, respectively. The conjugate of o is defined as $\overset{̅}{o} = Re (o) - \vec{o}$ $\overline{{o}}=\mathrm{Re}({o})-\overrightarrow{{o}}$ . The norm of o is defined by $| o | = \sqrt{\overset{̅}{o} o} = \sqrt{o \overset{̅}{o}} = \sqrt{\sum_{l = 0}^{7} o_{l}^{2}}$ $|{o}|=\sqrt{\overline{{o}}{o}}=\sqrt{{o}\overline{{o}}}=\sqrt{{\sum }_{\mathcal{l}=0}^7 {o}_{\mathcal{l}}^2}$ . 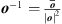The inverse of a non-zero octonion o is $o^{- 1} = \frac{\overset{̅}{o}}{| o |^{2}}$ ${{o}}^{-1}=\frac{\overline{{o}}}{|{o}{|}^2}$ .

The multiplication of 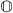$O$ $\mathbb{O}$ can be written in terms of the Euclidean inner product and the vector cross product in 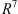$R^{7}$ ${R}^7$ , hereinafter denoted by • and ×, respectively. Concretely, as in [3], we have $ab = a_{0} b_{0} - \vec{a} \cdot \vec{b} + a_{0} \vec{b} + b_{0} \vec{a} + \vec{a} \times \vec{b} .$ ${ab}={a}_0{b}_0-\overrightarrow{{a}}\cdot \overrightarrow{{b}}+{a}_0\overrightarrow{{b}}+{b}_0\overrightarrow{{a}}+\overrightarrow{{a}}\times \overrightarrow{{b}}.$

Following [4], we recall that $a, b \in O$ ${a},{b}\in \mathbb{O}$ are perpendicular if $Re (a \overset{̅}{b}) = 0$ $\mathrm{Re}({a}\overline{{b}})=0$ . In particular, if $Re (a) = Re (b) = 0$ $\mathrm{Re}({a})=\mathrm{Re}({b})=0$ , then $a, b \in O$ ${a},{b}\in \mathbb{O}$ are perpendicular if $\vec{a} \cdot \vec{b} = 0$ $\overrightarrow{{a}}\cdot \overrightarrow{{b}}=0$ . Moreover, $a, b \in O$ ${a},{b}\in \mathbb{O}$ are parallel if $Im (a \overset{̅}{b}) = 0$ $\mathrm{Im}\enspace ({a}\overline{{b}})=0$ . In particular, if $Re (a) = Re (b) = 0$ $\mathrm{Re}({a})=\mathrm{Re}({b})=0$ , then $a, b \in O$ ${a},{b}\in O$ are parallel if $\vec{a} \times \vec{b} = 0$ $\overrightarrow{{a}}\times \overrightarrow{{b}}=0$ .

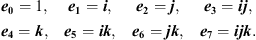
The elements of the basis of $O$ $\mathbb{O}$ can also be written as $\begin{array}{l} e_{0} = 1, & e_{1} = i, & e_{2} = j, & e_{3} = ij, \\ e_{4} = k, & e_{5} = ik, & e_{6} = jk, & e_{7} = ijk . \end{array}$ $\begin{array}{llll}{{e}}_{\mathbf{0}}=1,& {{e}}_{\mathbf{1}}={i},& {{e}}_{\mathbf{2}}={j},& {{e}}_{\mathbf{3}}={ij},\\ {{e}}_{\mathbf{4}}={k},& {{e}}_{\mathbf{5}}={ik},& {{e}}_{\mathbf{6}}={jk},& {{e}}_{\mathbf{7}}={ijk}.\\ & & & \end{array}$

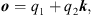The real octonion division algebra $O$ $\mathbb{O}$ , of dimension 8, can be constructed from the real quaternion division algebra $H$ $\mathbb{H}$ , of dimension 4, by the Cayley-Dickson doubling process where $O$ $\mathbb{O}$ contains $H$ $\mathbb{H}$ as a subalgebra. As a consequence, it is well known that any $o \in O$ ${o}\in \mathbb{O}$ can be written as $o = q_{1} + q_{2} k,$ ${o}={q}_1+{q}_2{k},$ (1) where $q_{1}, q_{2} \in H$ ${q}_1,{q}_2\in \mathbb{H}$ are of the form $a_{0} + a_{1} i + a_{2} j + a_{3} ij$ ${a}_0+{a}_1{i}+{a}_2{j}+{a}_3{ij}$ , with $a_{0}, a_{1}, a_{2}, a_{3} \in R$ ${a}_0,{a}_1,{a}_2,{a}_3\in \mathbb{R}$ .

The real quaternion division algebra $H$ $\mathbb{H}$ is algebraically isomorphic to the real matrix algebra of the matrices in (2), where ϕ(q) is a real matrix representation of a quaternion q.

Definition 1

[1] Let $q = q_{0} + q_{1} i + q_{2} j + q_{3} ij \in H$ $q={q}_0+{q}_1{i}+{q}_2{j}+{q}_3{ij}\in H$ . Then $ϕ (q) = [\begin{array}{l} q_{0} & - q_{1} & - q_{2} & - q_{3} \\ q_{1} & q_{0} & - q_{3} & q_{2} \\ q_{2} & q_{3} & q_{0} & - q_{1} \\ q_{3} & - q_{2} & q_{1} & q_{0} \end{array}] .$ $\phi (q)=\left[\begin{array}{llll}{q}_0& -{q}_1& -{q}_2& -{q}_3\\ {q}_1& {q}_0& -{q}_3& {q}_2\\ {q}_2& {q}_3& {q}_0& -{q}_1\\ {q}_3& -{q}_2& {q}_1& {q}_0\end{array}\right].$ (2)

Some important properties of the matrices in Definition 1 are recalled in Lemma 1.

Lemma 1

[1] Let $a, b \in H$ $a,b\in \mathbb{H}$ and $λ \in R$ $\lambda \in \mathbb{R}$ . Then

$a = b \Leftrightarrow ϕ (a) = ϕ (b)$ $a=b\iff \phi (a)=\phi (b)$ .
$\begin{matrix} ϕ (a + b) = ϕ (a) + ϕ (b), & ϕ (ab) = ϕ (a) ϕ (b), & ϕ (λ a) = λ ϕ (a), ϕ (1) = I_{4} \end{matrix}$ $\begin{array}{ccc}\phi \left(a+b\right)=\phi (a)+\phi (b),& \mathrm{\phi }\left({ab}\right)=\phi (a)\phi (b),& \phi \left(\lambda a\right)=\lambda \phi (a),\enspace \phi (1)={I}_4\end{array}$ .
$ϕ (\overset{̅}{a}) = ϕ^{T} (a)$ $\phi (\bar{a})={\phi }^T(a)$ .
$ϕ (a^{- 1}) = ϕ^{- 1} (a)$ $\phi ({a}^{-1})={\phi }^{-1}(a)$ , if $a \neq 0$ $a\ne 0$ .
$\det [ϕ (a)] = | a |^{4}$ $\mathrm{det}\left[\phi (a)\right]=|a{|}^4$ .

The real quaternion division algebra $H$ $\mathbb{H}$ is algebraically anti-isomorphic to the real matrix algebra of the matrices in (3), where τ(q) is another real matrix representation of a quaternion q.

Definition 2

[1] Let $q = q_{0} + q_{1} i + q_{2} j + q_{3} ij \in H$ $q={q}_0+{q}_1{i}+{q}_2{j}+{q}_3{ij}\in H$ . Then $τ (q) = K_{4} ϕ^{T} (q) K_{4} = [\begin{array}{l} q_{0} & - q_{1} & - q_{2} & - q_{3} \\ q_{1} & q_{0} & q_{3} & - q_{2} \\ q_{2} & - q_{3} & q_{0} & q_{1} \\ q_{3} & q_{2} & - q_{1} & q_{0} \end{array}],$ $\tau (q)={K}_4{\phi }^T(q){K}_4=\left[\begin{array}{llll}{q}_0& -{q}_1& -{q}_2& -{q}_3\\ {q}_1& {q}_0& {q}_3& -{q}_2\\ {q}_2& -{q}_3& {q}_0& {q}_1\\ {q}_3& {q}_2& -{q}_1& {q}_0\end{array}\right],$ (3) where K₄ = diag(1, −1, −1, −1).

Some relevant properties of the matrices in Definition 2 are recalled in Lemma 2.

Lemma 2

[1] Let $a, b \in H$ $a,b\in \mathbb{H}$ and $λ \in R$ $\lambda \in \mathbb{R}$ . Then

$a = b \Leftrightarrow τ (a) = τ (b)$ $a=b\iff \tau (a)=\tau (b)$ .
τ(a + b) = τ(a) + τ(b), τ(ab) = τ(b)τ(a), τ(λa) = λτ(a), τ(1) = I ₄.
$τ (\overset{̅}{a}) = τ^{T} (a)$ $\tau (\bar{a})={\tau }^T(a)$ .
$τ (a^{- 1}) = τ^{- 1} (a)$ $\tau ({a}^{-1})={\tau }^{-1}(a)$ , if $a \neq 0$ $a\ne 0$ .
$\det [τ (a)] = | a |^{4}$ $\mathrm{det}\left[\tau (a)\right]=|a{|}^4$ .

Due to the non-associativity, the octonion algebra cannot be isomorphic to the real matrix algebra with the usual multiplication. With the purpose of introducing a convenient matrix multiplication, we show another way of representing the octonions by a column matrix.

Definition 3

Let 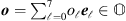$o = \sum_{l = 0}^{7} o_{l} e_{l} \in O$ ${o}={\sum }_{\mathcal{l}=0}^7{o}_{\mathcal{l}}{{e}}_{\mathcal{l}}\in \mathbb{O}$ . The column , vectorial or ket representation of o is $| o 〉 = [o_{0} o_{1} \dots o_{7}]^{T}$ $|{o}\right\rangle=[{o}_0\enspace {o}_1\enspace \cdots \enspace {o}_7{]}^T$ .

Based on the previous real matrix representations of a quaternion, Tian introduced the following pseudo real matrix representation of an octonion.

Definition 4

[1] Let $a = a' + a^{″} k \in O$ ${a}={a\prime}+{a}^{\prime\prime }{k}\in \mathbb{O}$ , where $a' = a_{0} + a_{1} i + a_{2} j + a_{3} ij, a^{″} = a_{4} + a_{5} i + a_{6} j + a_{7} ij \in H$ ${a\prime}={a}_0+{a}_1{i}+{a}_2{j}+{a}_3{ij},{a}^{\prime\prime }={a}_4+{a}_5{i}+{a}_6{j}+{a}_7{ij}\in \mathbb{H}$ . Then the 8 × 8 real matrix $ω (a) = [\begin{array}{l} ϕ (a') & - τ (a^{″}) K_{4} \\ ϕ (a^{″}) K_{4} & τ (a') \end{array}],$ $\omega ({a})=\left[\begin{array}{ll}\phi (a\mathrm{\prime})& -\tau ({a}^{\prime\prime }){K}_4\\ \phi ({a}^{\prime\prime }){K}_4& \tau (a\mathrm{\prime})\end{array}\right],$ (4) is called the left matrix representation of a over $R$ $\mathbb{R}$ , where K ₄ = diag(1, −1, −1, −1).

The meaning of the term left matrix representation comes from the following result.

Theorem 1

[1] Let $a, x \in O$ ${a},{x}\in \mathbb{O}$ . Then $| ax 〉 = ω (a) | x 〉$ $|{ax}\right\rangle=\omega ({a})|{x}\right\rangle$ .

Tian [1] introduced also the right matrix representation of an octonion a over $R$ $\mathbb{R}$ , which he denoted by $ν (a)$ $\nu ({a})$ . In this case, Tian proved that $| xa 〉 = ν (a) | x 〉$ $|{xa}\right\rangle=\nu ({a})|{x}\right\rangle$ .

Even though there are $a, b \in O$ ${a},{b}\in \mathbb{O}$ such that $ω (a) ω (b) \neq ω (ab)$ $\omega ({a})\omega ({b})\ne \omega ({ab})$ , there are still some properties which hold. These are recalled in Theorem 2.

Theorem 2

[1] Let $a, b \in O$ ${a},{b}\in \mathbb{O}$ , $λ \in R$ $\lambda \in \mathbb{R}$ . Then

$a = b \Leftrightarrow ω (a) = ω (b)$ ${a}={b}\iff \omega (\mathbf{a})=\omega (\mathbf{b})$ .
ω( a + b ) = ω( a ) + ω( b ), ω(λ a ) = λω( a ), ω(1) = I ₈.
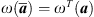$ω (\overset{̅}{a}) = ω^{T} (a)$ $\omega (\overline{{a}})={\omega }^T({a})$ .

3 Main results

In this section, the left matrix representation of an octonion over $R$ $\mathbb{R}$ is considered. First of all, given an octonion, the eigenvalues of its left matrix representation are computed.

Proposition 1

Let $a = a_{0} + \vec{a} \in O$ ${a}={a}_0+\overrightarrow{{a}}\in \mathbb{O}$ . Then the eigenvalues of the real matrix ω( a ) are $λ = a_{0} \pm i | \vec{a} |,$ $\lambda ={a}_0\pm {i}|\overrightarrow{{a}}|,$ each with algebraic multiplicity 4.

Proof. Given an octonion a, it can always be uniquely represented as $a = a_{0} + a' + a^{″} k$ ${a}={a}_0+a\mathrm{\prime}+{a}^{\prime\prime }{k}$ such that $a_{0} = Re (a)$ ${a}_0=\mathrm{Re}({a})$ , and where $a', a^{″} \in H$ $a\mathrm{\prime},{a}^{\prime\prime }\in H$ . The characteristic polynomial of ω( a ) is $\det (λ I_{8} - ω (a)) = \det (K_{8} (λ I_{8} - ω (a)) K_{8}),$ $\mathrm{det}\left(\lambda {I}_8-\omega \left({a}\right)\right)=\mathrm{det}\left({K}_8\left(\lambda {I}_8-\omega \left({a}\right)\right){K}_8\right),$ where K ₈ is the orthogonal matrix diag(1, −1, −1, −1, 1, 1, 1, 1) = diag(K ₄, I ₄). Hence, $\det (λ I_{8} - ω (a)) = \det ([\begin{array}{l} K_{4} & 0 \\ 0 & I_{4} \end{array}] [\begin{array}{l} ϕ (λ - a_{0} - a') & τ (a^{″}) K_{4} \\ - ϕ (a'') K_{4} & τ (λ - a_{0} - a') \end{array}] [\begin{array}{l} K_{4} & 0 \\ 0 & I_{4} \end{array}])$ $\mathrm{det}(\lambda {I}_8-\omega ({a}))=\mathrm{det}\left(\left[\begin{array}{ll}{K}_4& 0\\ 0& {I}_4\end{array}\right]\left[\begin{array}{ll}\phi (\lambda -{a}_0-a\mathrm{\prime})& \tau ({a}^{\prime\prime }){K}_4\\ -\phi (a\mathrm{\prime}\mathrm{\prime}){K}_4& \tau (\lambda -{a}_0-a\mathrm{\prime})\end{array}\right]\left[\begin{array}{ll}{K}_4& 0\\ 0& {I}_4\end{array}\right]\right)$ $= \det [\begin{array}{l} τ (λ - a_{0} + a') & ϕ (\overset{̅}{a^{″}}) \\ - ϕ (a^{″}) & τ (λ - a_{0} - a') \end{array}]$ $=\mathrm{det}\left[\begin{array}{ll}\tau (\lambda -{a}_0+a\mathrm{\prime})& \mathrm{\phi }(\overline{{a}^{\prime\prime }})\\ -\mathrm{\phi }({a}^{\prime\prime })& \tau (\lambda -{a}_0-a\mathrm{\prime})\end{array}\right]$ $= \det (τ (λ - a_{0} + a') τ (λ - a_{0} - a') + ϕ (\overset{̅}{a^{″}}) ϕ (a^{″})))$ $=\mathrm{det}\left(\tau (\lambda -{a}_0+a\mathrm{\prime})\tau (\lambda -{a}_0-a\mathrm{\prime})+\phi (\overline{{a}^{\prime\prime }})\phi ({a}^{\prime\prime }))\right)$ $= \det (τ ((λ - a_{0})^{2} + | a' |^{2}) + ϕ (| a^{″} |^{2}))$ $=\mathrm{det}\left(\tau \left((\lambda -{a}_0{)}^2+|a\mathrm{\prime}{|}^2\right)+\phi (|{a}^{\prime\prime }{|}^2)\right)$ $= \det (((λ - a_{0})^{2} + | a' |^{2}) I_{4} + | a^{″} |^{2} I_{4})$ $=\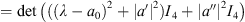mathrm{det}\left(((\lambda -{a}_0{)}^2+|a\mathrm{\prime}{|}^2){I}_4+|{a}^{\prime\prime }{|}^2{I}_4\right)$ $= \det (((λ - a_{0})^{2} + | \vec{a} |^{2}) I_{4})$ $=\mathrm{det}\left(((\lambda -{a}_0{)}^2+|\overrightarrow{{a}}{|}^2){I}_4\right)$ $= ((λ - a_{0})^{2} + | \vec{a} |^{2})^{4},$ $=((\lambda -{a}_0{)}^2+|\overrightarrow{{a}}{|}^2{)}^4,$ and the result follows.

The set of eigenvalues of ω( ab ) is equal to the set of eigenvalues of ω( a )ω( b ) since the characteristic polynomials are equal as can easily be seen. However, if we add an extra octonion c the set of eigenvalues of ω( ab + c ) and ω( a )ω( b ) + ω( c ) may differ.

We now study the eigenvalues of the matrix ω( a )ω( b ) + ω( c ), given three octonions a , b , and c .

Remark 1

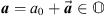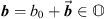Let $a = a_{0} + \vec{a} \in O$ ${a}={a}_0+\overrightarrow{{a}}\in \mathbb{O}$ and $b = b_{0} + \vec{b} \in O$ ${b}={b}_0+\overrightarrow{{b}}\in \mathbb{O}$ . Notice that 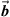$\vec{b}$ $\overrightarrow{{b}}$ can be decomposed into two parts: a part parallel to $\vec{a}$ $\overrightarrow{{a}}$ , denoted by ${\vec{b}}_{a}$ ${\overrightarrow{{b}}}_{{a}}$ ; and a part perpendicular to $\vec{a}$ $\overrightarrow{{a}}$ , denoted by ${\vec{b}}_{⊥}$ ${\overrightarrow{{b}}}_{\perp }$ . The parallel part is the projection of $\vec{b}$ $\overrightarrow{{b}}$ onto $\vec{a}$ $\overrightarrow{{a}}$ , which is defined as ${\vec{b}}_{a} \equiv {proj}_{\vec{a}} \vec{b} = \frac{\vec{a} \cdot \vec{b}}{\vec{a} \cdot \vec{a}} \vec{a} .$ ${\overrightarrow{{b}}}_{{a}}\equiv {\mathrm{proj}}_{\vec{a}}\overrightarrow{{b}}=\frac{\vec{a}\cdot \overrightarrow{{b}}}{\vec{a}\cdot \vec{a}}\vec{a}.$ The perpendicular part is given by ${\vec{b}}_{⊥} = \vec{b} - {\vec{b}}_{a}$ ${\overrightarrow{{b}}}_{\perp }=\overrightarrow{{b}}-{\overrightarrow{{b}}}_{\mathbf{a}}$ .

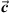Besides the projection of $\vec{b}$ $\overrightarrow{{b}}$ onto $\vec{a}$ $\overrightarrow{{a}}$ we will also consider the projection of $\vec{c}$ $\overrightarrow{{c}}$ over $Span (\vec{a}, \vec{b})$ $\mathrm{Span}(\overrightarrow{{a}},\overrightarrow{{b}})$ , i.e., the linear space generated by all linear combinations of $\vec{a}$ $\overrightarrow{{a}}$ and $\vec{b}$ $\overrightarrow{{b}}$ .

Remark 2

As ${\vec{b}}_{a} \in Span (\vec{a})$ ${\overrightarrow{{b}}}_{{a}}\in {Span}(\overrightarrow{{a}})$ and ${\vec{b}}_{a} \cdot {\vec{b}}_{⊥} = 0$ ${\overrightarrow{{b}}}_{{a}}\cdot {\overrightarrow{{b}}}_{\perp }=0$ , then $\begin{matrix} ab & = (a_{0} + \vec{a}) (b_{0} + {\vec{b}}_{a} + {\vec{b}}_{⊥}) \\ = a_{0} b_{0} + \vec{a} {\vec{b}}_{a} + b_{0} \vec{a} + a_{0} {\vec{b}}_{a} + a_{0} {\vec{b}}_{⊥} + \vec{a} {\vec{b}}_{⊥}, \end{matrix}$ $\begin{array}{cc}{ab}& =\left({a}_0+\overrightarrow{{a}}\right)\left({b}_0+{\overrightarrow{{b}}}_{{a}}+{\overrightarrow{{b}}}_{\perp }\right)\\ & ={a}_0{b}_0+\overrightarrow{{a}}{\overrightarrow{{b}}}_{\mathbf{a}}+{b}_0\overrightarrow{{a}}+{a}_0{\overrightarrow{{b}}}_{\mathbf{a}}+{a}_0{\overrightarrow{{b}}}_{\perp }+\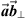overrightarrow{{a}}{\overrightarrow{{b}}}_{\perp },\end{array}$ where $a_{0} b_{0}, \vec{a} {\vec{b}}_{a} \in R$ ${a}_0{b}_0,\overrightarrow{{a}}{\overrightarrow{{b}}}_{{a}}\in R$ and $b_{0} \vec{a}, a_{0} {\vec{b}}_{a} \in Span (\vec{a})$ ${b}_0\overrightarrow{{a}},{a}_0{\overrightarrow{{b}}}_{{a}}\in {Span}(\overrightarrow{{a}})$ . Hence, it suffices to consider only the product $\vec{a} {\vec{b}}_{⊥}$ $\overrightarrow{{a}}{\overrightarrow{{b}}}_{\perp }$ since the remaining terms can be added to c .

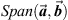The pure octonion $\vec{c}$ $\overrightarrow{{c}}$ can be decomposed in two parts, one in $Span (\vec{a}, \vec{b})$ ${Span}(\overrightarrow{{a}},\overrightarrow{{b}})$ and the other perpendicular to it. 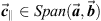In this case, we can write $\vec{c} = {\vec{c}}_{∥} + {\vec{c}}_{⊥}$ $\overrightarrow{{c}}={\overrightarrow{{c}}}_{\parallel }+{\overrightarrow{{c}}}_{\perp }$ , where ${\vec{c}}_{∥} \in Span (\vec{a}, \vec{b})$ ${\overrightarrow{{c}}}_{\parallel }\in {Span}(\overrightarrow{{a}},\overrightarrow{{b}})$ and ${\vec{c}}_{∥} \cdot {\vec{c}}_{⊥} = 0$ ${\overrightarrow{{c}}}_{\parallel }\cdot {\overrightarrow{{c}}}_{\perp }=0$ . 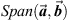The parallel part is the projection of $\vec{c}$ $\overrightarrow{{c}}$ onto $Span (\vec{a}, \vec{b})$ ${Span}(\overrightarrow{{a}},\overrightarrow{{b}})$ and is given by 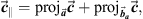${\vec{c}}_{∥} = {proj}_{\vec{a}} \vec{c} + {proj}_{{\vec{b}}_{a}} \vec{c},$ ${\overrightarrow{{c}}}_{\parallel }={\mathrm{proj}}_{\overrightarrow{{a}}}\overrightarrow{{c}}+{\mathrm{proj}}_{{\overrightarrow{{b}}}_{{a}}}\overrightarrow{{c}},$ and the perpendicular part is naturally ${\vec{c}}_{⊥} = \vec{c} - {\vec{c}}_{∥}$ ${\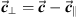overrightarrow{{c}}}_{\perp }=\overrightarrow{{c}}-{\overrightarrow{{c}}}_{\parallel }$ .

Proposition 2

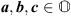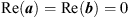Let $a, b, c \in O$ ${a},{b},{c}\in \mathbb{O}$ such that $Re (a) = Re (b) = 0$ $\mathrm{Re}({a})=\mathrm{Re}({b})=0$ , and the imaginary part of a and b are perpendicular. Then the eigenvalues of the real matrix ω( a )ω( b ) + ω( c ) are $Re (c) \pm i \sqrt{(| a | | b | \pm | c_{⊥} |)^{2} + | c_{∥} |^{2}},$ $\mathrm{Re}({c})\pm {i}\sqrt{(|{a}||{b}|\pm |{{c}}_{\perp }|{)}^2+|{{c}}_{\parallel }{|}^2},$ (5) where c _∥ is the projection of c onto Span( a , b ) and $c_{⊥} = c - c_{∥}$ ${{c}}_{\perp }={c}-{{c}}_{\parallel }$ , each with algebraic multiplicity 2.

Proof. Without loss of generality, we consider a = a i and b = b j . Hence, $\begin{matrix} ω (a) ω (b) & = [\begin{array}{l} ϕ (a i) & 0 \\ 0 & τ (a i) \end{array}] [\begin{array}{l} ϕ (b j) & 0 \\ 0 & τ (b j) \end{array}] \\ = [\begin{array}{l} ϕ (a i) ϕ (b j) & 0 \\ 0 & τ (a i) τ (b j) \end{array}] \end{matrix} .$ $\begin{array}{cc}\omega \left({a}\right)\omega \left({b}\right)& =\left[\begin{array}{ll}\phi \left(a{i}\right)& 0\\ 0& \tau \left(a{i}\right)\end{array}\right]\left[\begin{array}{ll}\phi \left(b{j}\right)& 0\\ 0& \tau \left(b{j}\right)\end{array}\right]\\ & =\left[\begin{array}{ll}\phi (a{i})\phi (b\mathbf{j})& 0\\ 0& \tau (a\mathbf{i})\tau (b\mathbf{j})\end{array}\right]\end{array}.$

By Lemmas 1 and 2, we have $ω (a) ω (b) = [\begin{array}{l} ϕ (ab ij) & 0 \\ 0 & τ (- ab ij) \end{array}] .$ $\omega ({a})\omega ({b})=\left[\begin{array}{ll}\phi ({ab}{ij})& 0\\ 0& \tau (-{ab}{ij})\end{array}\right].$ (6) Let $c = c_{0} + c_{1} i + c_{2} j + c_{3} ij + c^{″} k$ ${c}={c}_0+{c}_1{i}+{c}_2{j}+{c}_3{ij}+{c}^{\prime\prime }{k}$ , where $c^{″} \in H$ ${c}^{\prime\prime }\in H$ . Then $ω (c) = [\begin{array}{l} ϕ (c_{0} + c_{1} i + c_{2} j + c_{3} ij) & - τ (c^{″}) K_{4} \\ ϕ (c^{″}) K_{4} & τ (c_{0} + c_{1} i + c_{2} j + c_{3} ij) \end{array}] .$ $\omega ({c})=\left[\begin{array}{ll}\phi ({c}_0+{c}_1{i}+{c}_2{j}+{c}_3{ij})& -\tau ({c}^{\prime\prime }){K}_4\\ \phi ({c}^{\prime\prime }){K}_4& \tau ({c}_0+{c}_1{i}+{c}_2{j}+{c}_3{ij})\end{array}\right].$ (7)

Taking into account (6) and (7), we obtain $ω (a) ω (b) + ω (c) = [\begin{array}{l} ϕ (c_{0} + c_{1} i + c_{2} j + (c_{3} + ab) ij) & - τ (c^{″}) K_{4} \\ ϕ (c^{″}) K_{4} & τ (c_{0} + c_{1} i + c_{2} j + (c_{3} - ab) ij) \end{array}] .$ $\omega \left({a}\right)\omega \left({b}\right)+\omega \left({c}\right)=\left[\begin{array}{ll}\phi \left({c}_0+{c}_1{i}+{c}_2{j}+\left({c}_3+{ab}\right){ij}\right)& -\tau \left({c}^{\prime\prime }\right){K}_4\\ \phi \left({c}^{\prime\prime }\right){K}_4& \tau \left({c}_0+{c}_1{i}+{c}_2{j}+\left({c}_3-{ab}\right){ij}\right)\end{array}\right].$

The characteristic polynomial of ω( a )ω( b ) + ω( c ) is $p (λ) = \det (ω (a) ω (b) + ω (c) - λ I_{8}) = \det (K_{8} (ω (a) ω (b) + ω (c) - λ I_{8}) K_{8}),$ $p\left(\lambda \right)=\mathrm{det}\left(\omega \left({a}\right)\omega \left({b}\right)+\omega \left({c}\right)-\lambda {I}_8\right)=\mathrm{det}\left({K}_8\left(\omega \left({a}\right)\omega \left({b}\right)+\omega \left({c}\right)-\lambda {I}_8\right){K}_8\right),$ where K₈ is the orthogonal matrix diag(1, −1, −1, −1, 1, 1, 1, 1) = diag(K ₄, I ₄). Hence, $p (λ) = \det [\begin{array}{l} τ (c_{0} - λ - c_{1} i - c_{2} j - (c_{3} + ab) ij) & - ϕ (\overset{̅}{c^{″}}) \\ ϕ (c^{″}) & τ (c_{0} - λ + c_{1} i + c_{2} j + (c_{3} - ab) ij) \end{array}],$ $p(\lambda )=\mathrm{det}\left[\begin{array}{ll}\tau ({c}_0-\lambda -{c}_1{i}-{c}_2{j}-({c}_3+{ab}){ij})& -\phi (\overline{{c}^{\prime\prime }})\\ \phi ({c}^{\prime\prime })& \tau ({c}_0-\lambda +{c}_1{i}+{c}_2{j}+({c}_3-{ab}){ij})\end{array}\right],$ which results in $p (λ) = \det (τ ((c_{0} - λ)^{2} + c_{1}^{2} + c_{2}^{2} + c_{3}^{2} - (ab)^{2} + 2 ab (c_{2} i - c_{1} j - (c_{0} - λ) ij)) + ϕ (| c^{″} |^{2})),$ $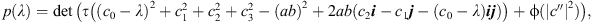p(\lambda )=\mathrm{det}\left(\tau \left(({c}_0-\lambda {)}^2+{c}_1^2+{c}_2^2+{c}_3^2-({ab}{)}^2+2{ab}({c}_2{i}-{c}_1{j}-({c}_0-\lambda ){ij})\right)+\mathrm{\phi }(|{c}^{\prime\prime }{|}^2)\right),$ and, since $ϕ (| c^{″} |^{2}) = τ (| c^{″} |^{2})$ $\mathrm{\phi }(|{c}^{\prime\prime }{|}^2)=\tau (|{c}^{\prime\prime }{|}^2)$ , gives $p (λ) = \det (τ ((c_{0} - λ)^{2} + | c_{∥} |^{2} + | c_{⊥} |^{2} - (ab)^{2} + 2 ab (c_{2} i - c_{1} j - (c_{0} - λ) ij))),$ $p(\lambda )=\mathrm{det}\left(\tau \left(({c}_0-\lambda {)}^2+|{{c}}_{\parallel }{|}^2+|{{c}}_{\perp }{|}^2-({ab}{)}^2+2{ab}({c}_2{i}-{c}_1{j}-({c}_0-\lambda ){ij})\right)\right),$ where $c_{∥} = c_{1} i + c_{2} j$ ${{c}}_{\parallel }={c}_1{i}+{c}_2{j}$ and $c_{⊥} = c_{3} ij + c^{″} k$ ${{c}}_{\perp }={c}_3{ij}+{c}^{\prime\prime }{k}$ . By Lemma 2, we have $\begin{matrix} p (λ) & = {[((c_{0} - λ)^{2} + | c_{∥} |^{2} + | c_{⊥} |^{2} - (ab)^{2})^{2} + 4 (ab)^{2} (| c_{∥} |^{2} + (c_{0} - λ)^{2})]}^{2} \\ \begin{matrix} = [((c_{0} - λ)^{2} + | c_{∥} |^{2})^{2} + 2 ((c_{0} - λ)^{2} + | c_{∥} |^{2}) (| c_{⊥} |^{2} - (ab)^{2}) + (| c_{⊥} |^{2} - (ab)^{2})^{2} + {4 (ab)^{2} (| c_{∥} |^{2} + (c_{0} - λ)^{2})]}^{2} \\ = [((c_{0} - λ)^{2} + | c_{∥} |^{2})^{2} + 2 ((c_{0} + λ)^{2} + | c_{∥} |^{2}) (| c_{⊥} |^{2} - (ab)^{2}) + (| c_{⊥} |^{2} (ab)^{2})^{2} - {4 (ab)^{2} | c_{⊥} |^{2}]}^{2} \end{matrix} \\ \begin{matrix} = {[((c_{0} - λ)^{2} + | c_{∥} |^{2} + | c_{⊥} |^{2} + (ab)^{2})^{2} - 4 (ab)^{2} | c_{⊥} |^{2}]}^{2} \\ = {[((c_{0} - λ)^{2} + | \vec{c} |^{2} + (ab)^{2})^{2} - 4 (ab)^{2} | c_{⊥} |^{2}]}^{2}, \end{matrix} \end{matrix}$ $\begin{array}{cc}p(\lambda )& ={\left[(({c}_0-\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2+|{\mathbf{c}}_{\perp }{|}^2-({ab}{)}^2{)}^2+4({ab}{)}^2(|{\mathbf{c}}_{\parallel }{|}^2+({c}_0-\lambda {)}^2)\right]}^2\\ & \begin{array}{c}=\left[(({c}_0-\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2{)}^2+2(({c}_0-\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2)(|{\mathbf{c}}_{\perp }{|}^2-({ab}{)}^2)+(|{\mathbf{c}}_{\perp }{|}^2-({ab}{)}^2{)}^2\right.+{\left.4({ab}{)}^2(|{\mathbf{c}}_{\parallel }{|}^2+({c}_0-\lambda {)}^2)\right]}^2\\ =\left[(({c}_0-\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2{)}^2+2(({c}_0+\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2)(|{\mathbf{c}}_{\perp }{|}^2-({ab}{)}^2)+(|{\mathbf{c}}_{\perp }{|}^2({ab}{)}^2{)}^2-\right.{\left.4({ab}{)}^2|{\mathbf{c}}_{\perp }{|}^2\right]}^2\end{array}\\ & \begin{array}{c}={\left[(({c}_0-\lambda {)}^2+|{\mathbf{c}}_{\parallel }{|}^2+|{\mathbf{c}}_{\perp }{|}^2+({ab}{)}^2{)}^2-4({ab}{)}^2|{\mathbf{c}}_{\perp }{|}^2\right]}^2\\ ={\left[(({c}_0-\lambda {)}^2+|\overrightarrow{{c}}{|}^2+({ab}{)}^2{)}^2-4({ab}{)}^2|{\mathbf{c}}_{\perp }{|}^2\right]}^2,\end{array}\end{array}$ and the result follows.

The following corollary may be useful to improve the localization of eigenvalues of octonionic matrices and zeros of octonionic polynomials whenever such products occur.

Corollary 2.1

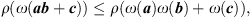Let $a, b, c \in O$ ${a},{b},{c}\in \mathbb{O}$ . Then $ρ (ω (ab + c)) \leq ρ (ω (a) ω (b) + ω (c)),$ $\rho \left(\omega ({ab}+{c})\right)\le \rho \left(\omega ({a})\omega ({b})+\omega ({c})\right),$ (8) where ρ(•) stands for the spectral radius.

Proof. By Proposition 2, we obtain 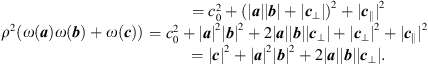$\begin{matrix} ρ^{2} (ω (a) ω (b) + ω (c)) \end{matrix} \begin{matrix} = c_{0}^{2} + (| a | | b | + | c_{⊥} |)^{2} + | c_{∥} |^{2} \\ = c_{0}^{2} + | a |^{2} | b |^{2} + 2 | a | | b | | c_{⊥} | + | c_{⊥} |^{2} + | c_{∥} |^{2} \\ = | c |^{2} + | a |^{2} | b |^{2} + 2 | a | | b | | c_{⊥} | . \end{matrix}$ $\begin{array}{c}{\rho }^2\left(\omega \left({a}\right)\omega \left({b}\right)+\omega \left({c}\right)\right)\\ \\ \end{array}\begin{array}{c}={c}_0^2+(|{a}||{b}|+|{{c}}_{\perp }|{)}^2+|{{c}}_{\parallel }{|}^2\\ ={c}_0^2+|{a}{|}^2|{b}{|}^2+2|{a}||{b}||{{c}}_{\perp }|+|{{c}}_{\perp }{|}^2+|{{c}}_{\parallel }{|}^2\\ =|{c}{|}^2+|{a}{|}^2|{b}{|}^2+2|{a}||{b}||{{c}}_{\perp }|.\end{array}$

Furthermore, the eigenvalues of ω( ab + c ) are all equal in modulus and satisfy $\begin{matrix} ρ^{2} (ω (ab + c)) & = (ab + c) (\overset{̅}{ab + c}) \\ = | a |^{2} | b |^{2} + | c |^{2} + 2 Re ((ab) \overset{̅}{c}) . \end{matrix}$ $\begin{array}{cc}{\rho }^2(\omega ({ab}+{c}))& =({ab}+{c})(\overline{{ab}+{c}})\\ & =|{a}{|}^2|{b}{|}^2+|{c}{|}^2+2\mathrm{Re}(({ab})\overline{{c}}).\end{array}$

Without loss of generality, we can consider a = a i and b = b j . If 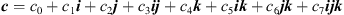$c = c_{0} + c_{1} i + c_{2} j + c_{3} ij + c_{4} k + c_{5} ik + c_{6} jk + c_{7} ijk$ ${c}={c}_0+{c}_1{i}+{c}_2{j}+{c}_3{ij}+{c}_4{k}+{c}_5{ik}+{c}_6{jk}+{c}_7{ijk}$ . Hence, we arrive at $\begin{matrix} ρ^{2} (ω (ab + c)) & = | a |^{2} | b |^{2} + | c |^{2} + 2 Re ((ab) \overset{̅}{c}) \\ = (ab)^{2} + | c |^{2} + 2 ab c_{3} \\ \begin{matrix} \leq (ab)^{2} + | c |^{2} + 2 | ab | \sqrt{c_{3}^{2} + c_{4}^{2} + c_{5}^{2} + c_{6}^{2} + c_{7}^{2}} \\ = (ab)^{2} + | c |^{2} + 2 | ab | | c_{⊥} | \\ = ρ^{2} (ω (a) ω (b) + ω (c)), \end{matrix} \end{matrix}$ $\begin{array}{cc}{\rho }^2\left(\omega \left({ab}+{c}\right)\right)& =|{a}{|}^2|{b}{|}^2+|{c}{|}^2+2\enspace \mathrm{Re}\enspace (({ab})\overline{{c}})\\ & =({ab}{)}^2+|\mathbf{c}{|}^2+2{ab}{c}_3\\ & \begin{array}{c}\le ({ab}{)}^2+|\mathbf{c}{|}^2+2|{ab}|\sqrt{{c}_3^2+{c}_4^2+{c}_5^2+{c}_6^2+{c}_7^2}\\ =({ab}{)}^2+|\mathbf{c}{|}^2+2|{ab}||{\mathbf{c}}_{\perp }|\\ ={\rho }^2\left(\omega (\mathbf{a})\omega (\mathbf{b})+\omega (\mathbf{c})\right),\end{array}\end{array}$ and the result follows.

Example 3.1

Let $a = 1 + i + k + ijk, b = - 1 + 2 ij - ik + 3 ijk, c = 2 + i + j + 2 k - 5 ik + jk - 12 ijk .$ ${a}=1+{i}+{k}+{ijk},\enspace {b}=-1+2{ij}-{ik}+3{ijk},\enspace {c}=2+{i}+{j}+2{k}-5{ik}+{jk}-12{ijk}.$

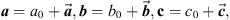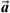To apply (5) , we have to take into account Remarks 1 and 2, and rewrite a , b and c as $a = a_{0} + \vec{a}, b = b_{0} + \vec{b}, c = c_{0} + \vec{c},$ ${a}={a}_0+\overrightarrow{{a}},{b}={b}_0+\overrightarrow{{b}},\mathbf{c}={c}_0+\overrightarrow{{c}},$ where $\vec{a}$ $\overrightarrow{{a}}$ , $\vec{b}$ $\overrightarrow{{b}}$ and $\vec{c}$ $\overrightarrow{{c}}$ are the imaginary parts of a , b and c , respectively.

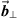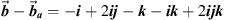Computing ${\vec{b}}_{a}$ ${\overrightarrow{{b}}}_{{a}}$ , the projection of $\vec{b}$ $\overrightarrow{{b}}$ onto $\vec{a}$ $\overrightarrow{{a}}$ , we obtain ${\vec{b}}_{a} = \vec{a}$ ${\overrightarrow{{b}}}_{{a}}=\overrightarrow{{a}}$ . Thus, the orthogonal part ${\vec{b}}_{⊥}$ ${\overrightarrow{{b}}}_{\perp }$ is equal to $\vec{b} - {\vec{b}}_{a} = - i + 2 ij - k - ik + 2 ijk$ $\overrightarrow{{b}}-{\overrightarrow{{b}}}_{{a}}=-{i}+2{ij}-{k}-{ik}+2{ijk}$ .

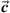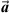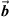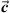The projections of $\vec{c}$ $\overrightarrow{{c}}$ onto $\vec{a}$ $\overrightarrow{{a}}$ and $\vec{b}$ $\overrightarrow{{b}}$ are, respectively ${\vec{c}}_{a} = - 3 \vec{a}$ ${\overrightarrow{{c}}}_{{a}}=-3\overrightarrow{{a}}$ and ${\vec{c}}_{b_{⊥}} = - 2 {\vec{b}}_{⊥}$ ${\overrightarrow{{c}}}_{{{b}}_{\perp }}=-2{\overrightarrow{{b}}}_{\perp }$ . 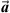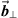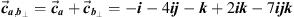Hence, the projection of $\vec{c}$ $\overrightarrow{{c}}$ on the space of $\vec{a}$ $\overrightarrow{{a}}$ and ${\vec{b}}_{⊥}$ ${\overrightarrow{{b}}}_{\perp }$ is ${\vec{c}}_{a, b_{⊥}} = {\vec{c}}_{a} + {\vec{c}}_{b_{⊥}} = - i - 4 ij - k + 2 ik - 7 ijk$ ${\overrightarrow{{c}}}_{{a},{{b}}_{\perp }}={\overrightarrow{{c}}}_{{a}}+{\overrightarrow{{c}}}_{{{b}}_{\perp }}=-{i}-4{ij}-{k}+2{ik}-7{ijk}$ . This implies that for the orthogonal part we have ${\vec{c}}_{⊥} = \vec{c} - {\vec{c}}_{a, b_{⊥}} = 2 i + j + 4 ij + 3 k - 7 ik + jk - 5 ijk$ ${\overrightarrow{{c}}}_{\perp }=\overrightarrow{{c}}-{\overrightarrow{{c}}}_{{a},{{b}}_{\perp }}=2{i}+{j}+4{ij}+3{k}-7{ik}+{jk}-5{ijk}$ .

Taking all together, we have $ab + c = (a_{0} + \vec{a}) (b_{0} + {\vec{b}}_{a} + {\vec{b}}_{⊥}) + c_{0} + {\vec{c}}_{a, b_{⊥}} + {\vec{c}}_{⊥}$ ${ab}+{c}=({a}_0+\overrightarrow{{a}})({b}_0+{\overrightarrow{{b}}}_{\mathbf{a}}+{\overrightarrow{{b}}}_{\perp })+{c}_0+{\overrightarrow{{c}}}_{{a},{{b}}_{\perp }}+{\overrightarrow{{c}}}_{\perp }$ $= \vec{a} {\vec{b}}_{⊥} + (c_{0} + a_{0} b_{0} + \vec{a} {\vec{b}}_{a}) + ({\vec{c}}_{a, b_{⊥}} + a_{0} {\vec{b}}_{a} + b_{0} \vec{a} + a_{0} {\vec{b}}_{⊥}) + {\vec{c}}_{⊥},$ $=\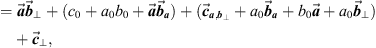overrightarrow{{a}}{\overrightarrow{{b}}}_{\perp }+({c}_0+{a}_0{b}_0+\overrightarrow{{a}}{\overrightarrow{{b}}}_{{a}})+({\overrightarrow{{c}}}_{{a},{{b}}_{\perp }}+{a}_0{\overrightarrow{{b}}}_{{a}}+{b}_0\overrightarrow{{a}}+{a}_0{\overrightarrow{{b}}}_{\perp })+{\overrightarrow{{c}}}_{\perp },$ where $c_{0} + a_{0} b_{0} + \vec{a} {\vec{b}}_{a}$ ${c}_0+{a}_0{b}_0+\overrightarrow{{a}}{\overrightarrow{{b}}}_{{a}}$ is real and ${\vec{c}}_{a, b_{⊥}} + a_{0} {\vec{b}}_{a} + b_{0} \vec{a} + a_{0} {\vec{b}}_{⊥} \in Span (\vec{a}, b_{⊥})$ ${\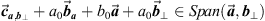overrightarrow{{c}}}_{{a},{{b}}_{\perp }}+{a}_0{\overrightarrow{{b}}}_{{a}}+{b}_0\overrightarrow{{a}}+{a}_0{\overrightarrow{{b}}}_{\perp }\in {Span}(\overrightarrow{{a}},{{b}}_{\perp })$ . So $ab + c = \vec{a} b_{⊥} + C_{0} + {\vec{c}}_{∥} + {\vec{c}}_{⊥},$ ${ab}+{c}=\overrightarrow{{a}}{{b}}_{\perp }+{C}_0+{\overrightarrow{{c}}}_{\parallel }+{\overrightarrow{{c}}}_{\perp },$ (9) where $C_{0} = c_{0} + a_{0} b_{0} + \vec{a} {\vec{b}}_{a} = - 2$ ${C}_0={c}_0+{a}_0{b}_0+\overrightarrow{{a}}{\overrightarrow{{b}}}_{{a}}=-2$ , ${\vec{c}}_{∥} = {\vec{c}}_{a, b_{⊥}} + a_{0} {\vec{b}}_{a} + b_{0} \vec{a} + a_{0} {\vec{a}}_{⊥} = - 2 i - 2 ij - 2 k + ik - 5 ijk$ ${\overrightarrow{{c}}}_{\parallel }={\overrightarrow{{c}}}_{{a},{{b}}_{\perp }}+{a}_0{\overrightarrow{{b}}}_{{a}}+{b}_0\overrightarrow{{a}}+{a}_0{\overrightarrow{{a}}}_{\perp }=-2{i}-2{ij}-2{k}+{ik}-5{ijk}$ , and ${\vec{c}}_{⊥} = 2 i + j + 4 ij + 3 k - 7 ik + jk - 5 ijk$ ${\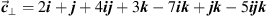overrightarrow{{c}}}_{\perp }=2{i}+{j}+4{ij}+3{k}-7{ik}+{jk}-5{ijk}$ .

We are now in condition to apply Proposition 2, from which we obtain the eigenvalues of $ω (a) ω (b) + ω (c) = [\begin{matrix} - 2 & 1 & 0 & - 5 & - 4 & 6 & - 4 & 12 \\ - 1 & - 2 & 1 & - 2 & 6 & 0 & - 8 & - 4 \\ 0 & - 1 & - 2 & - 1 & 2 & 8 & - 2 & - 6 \\ 5 & 2 & 1 & - 2 & 12 & - 2 & 6 & 2 \\ 4 & - 6 & - 2 & - 12 & - 2 & 1 & - 2 & - 5 \\ - 6 & 0 & - 8 & 2 & - 1 & - 2 & - 1 & - 4 \\ 4 & 8 & - 2 & - 6 & 2 & 1 & - 2 & 1 \\ - 12 & 4 & 6 & - 2 & 5 & 4 & - 1 & - 2 \end{matrix}] .$ $\omega ({a})\omega ({b})+\omega ({c})=\left[\begin{array}{cccccccc}-2& 1& 0& -5& -4& 6& -4& 12\\ -1& -2& 1& -2& 6& 0& -8& -4\\ 0& -1& -2& -1& 2& 8& -2& -6\\ 5& 2& 1& -2& 12& -2& 6& 2\\ 4& -6& -2& -12& -2& 1& -2& -5\\ -6& 0& -8& 2& -1& -2& -1& -4\\ 4& 8& -2& -6& 2& 1& -2& 1\\ -12& 4& 6& -2& 5& 4& -1& -2\end{array}\right].$

The eigenvalues are 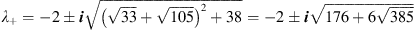$λ_{+} = - 2 \pm i \sqrt{{(\sqrt{33} + \sqrt{105})}^{2} + 38} = - 2 \pm i \sqrt{176 + 6 \sqrt{385}}$ ${\lambda }_{+}=-2\pm {i}\sqrt{{\left(\sqrt{33}+\sqrt{105}\right)}^2+38}=-2\pm {i}\sqrt{176+6\sqrt{385}}$ and $λ_{-} = - 2 \pm i \sqrt{{(\sqrt{33} - \sqrt{105})}^{2} + 38} = - 2 \pm i \sqrt{176 - 6 \sqrt{385}}$ ${\lambda }_{-}=-2\pm {i}\sqrt{{\left(\sqrt{33}-\sqrt{105}\right)}^2+38}=-2\pm {i}\sqrt{176-6\sqrt{385}}$ , while the eigenvalues of $ω (ab + c)$ $\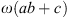omega ({ab}+c)$ are $λ = - 2 \pm i \sqrt{238}$ $\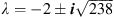lambda =-2\pm {i}\sqrt{238}$ .

As predicted by Corollary 2.1, 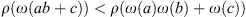$ρ (ω (ab + c)) < ρ (ω (a) ω (b) + ω (c))$ $\rho (\omega ({ab}+c)) < \rho (\omega (a)\omega (b)+\omega (c))$ , since $ρ (ω (ab + c)) = | λ | = 11 \sqrt{2}$ $\rho (\omega ({ab}+c))=|\lambda |=11\sqrt{2}$ and $ρ (ω (a) ω (b) + ω (c)) = | λ_{+} | = \sqrt{180 + 6 \sqrt{385}}$ $\rho (\omega (a)\omega (b)+\omega (c))=|{\lambda }_{+}|=\sqrt{180+6\sqrt{385}}$ .

Acknowledgments

The authors are very thankful to the anonymous referee for his valuable suggestions towards the improvement of this paper.

R. Serôdio and P.D. Beites were supported by Fundação para a Ciência e a Tecnologia (Portugal), project UID/MAT/00212/2013 of the Centro de Matemática e Aplicações da Universidade da Beira Interior (CMA-UBI). P.D. Beites was also supported by the research project MTM2017-83506-C2-2-P (Spain).

References

Tian Y (2000), Matrix representations of octonions and their applications. Adv Appl Clifford Algebras 10, 61–90. [CrossRef] [Google Scholar]
Beites PD, Nicolás AP, Vitória J (2017), On skew-symmetric matrices related to the vector cross product in R⁷. Electron J Linear Algebra 32, 138–150. [CrossRef] [Google Scholar]
Leite FS (1993), The geometry of hypercomplex matrices. Linear Multilinear Algebra 34, 123–132. [CrossRef] [Google Scholar]
Ward JP (1997), Quaternions and Cayley numbers, Kluwer, Dordrecht. [CrossRef] [Google Scholar]

Cite this article as: Serôdio R, Beites P & Vitória J 2019. Eigenvalues of matrices related to the octonions. 4open, 2, 16.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Tian Y (2000), Matrix representations of octonions and their applications. Adv Appl Clifford Algebras 10, 61–90. [CrossRef] [Google Scholar]

[2] Beites PD, Nicolás AP, Vitória J (2017), On skew-symmetric matrices related to the vector cross product in R⁷. Electron J Linear Algebra 32, 138–150. [CrossRef] [Google Scholar]

[3] Leite FS (1993), The geometry of hypercomplex matrices. Linear Multilinear Algebra 34, 123–132. [CrossRef] [Google Scholar]

[4] Ward JP (1997), Quaternions and Cayley numbers, Kluwer, Dordrecht. [CrossRef] [Google Scholar]