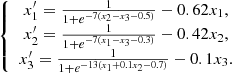| Issue |
4open
Volume 3, 2020
|
|
|---|---|---|
| Article Number | 8 | |
| Number of page(s) | 9 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2020009 | |
| Published online | 04 August 2020 | |
Research Article
Remarks on GRN-type systems
1
Daugavpils University, Parades Street 1, 5400 Daugavpils, Latvia
2
Institute of Mathematics and Computer Science, University of Latvia, Rainis Boulevard 29, 1459 Riga, Latvia
* Corresponding author: felix@latnet.lv
Received:
18
March
2020
Accepted:
19
July
2020
Systems of ordinary differential equations that appear in gene regulatory networks theory are considered. We are focused on asymptotical behavior of solutions. There are stable critical points as well as attractive periodic solutions in two-dimensional and three-dimensional systems. Instead of considering multiple parameters (10 in a two-dimensional system) we focus on typical behaviors of nullclines. Conclusions about possible attractors are made.
Mathematics Subject Classification: 34C60 / 34D45 / 92B20
Key words: Ordinary differential equations / Genetic regulatory networks / Attractors
© E. Brokan and F. Sadyrbaev, Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
We consider systems of ordinary differential equations (ODE) of the form,
 (1)where all parameters w
ij
and θ
i
are real numbers, μ
i
and γ
i
are positive numbers. The function
(1)where all parameters w
ij
and θ
i
are real numbers, μ
i
and γ
i
are positive numbers. The function 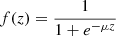 is a sigmoidal function,1 which is defined for all z ∈ R, strictly increasing from zero to unity and has exactly one inflection point. Some other sigmoidal function, such as the Gompertz function2
is a sigmoidal function,1 which is defined for all z ∈ R, strictly increasing from zero to unity and has exactly one inflection point. Some other sigmoidal function, such as the Gompertz function2
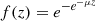 , also can be used in the above system [1]. The system (1) is often used in models of various real-world phenomena. It has appeared (for n = 2) in the paper by Wilson and Cowan [2] as a simplified model of interaction of two populations of neurons. The n dimensional version is believed to describe the interrelations in genetic regulatory networks (GRN in short), that is, probably, the most popular object related to the system (1). A GRN can be thought of as a complicated network existing in living cells that instantly remodel themselves. Every element of this network, gene, interacts with others and the character of this interaction is described by the so-called regulatory matrix W. The positive entries w
ij
of W mean activation of x
i
by x
j
. The negative ones mean inhibition. The zero entries are for no relation. The dynamics of the entire GRN is described by the system (1). Future states of a network are of primary interest. To understand them, one has to investigate possible attractors of the system (1). There are various mathematical models of GRN, for instance, models, formulated in terms of graph theory, Boolean algebras, etc. The possibility of studying future network states is a significant advantage of models based on systems of differential equations. For a description of genes and genome, we invite the reader to consult papers and book chapters in [3–6].
, also can be used in the above system [1]. The system (1) is often used in models of various real-world phenomena. It has appeared (for n = 2) in the paper by Wilson and Cowan [2] as a simplified model of interaction of two populations of neurons. The n dimensional version is believed to describe the interrelations in genetic regulatory networks (GRN in short), that is, probably, the most popular object related to the system (1). A GRN can be thought of as a complicated network existing in living cells that instantly remodel themselves. Every element of this network, gene, interacts with others and the character of this interaction is described by the so-called regulatory matrix W. The positive entries w
ij
of W mean activation of x
i
by x
j
. The negative ones mean inhibition. The zero entries are for no relation. The dynamics of the entire GRN is described by the system (1). Future states of a network are of primary interest. To understand them, one has to investigate possible attractors of the system (1). There are various mathematical models of GRN, for instance, models, formulated in terms of graph theory, Boolean algebras, etc. The possibility of studying future network states is a significant advantage of models based on systems of differential equations. For a description of genes and genome, we invite the reader to consult papers and book chapters in [3–6].
One of the main features of GRN is the ability to adapt to changes in the environment. Understanding of the mechanism of adaptation is important for designers of artificial networks. The telecommunication networks are of this kind. In the works by several authors, for instance, [7, 8], the self-organization of GRN is considered as a source of ideas for designers of practical networks.
It was proposed [8] to use the attractor selection as the principal mechanism for the creation of virtual network topology (VNT), which could realize the rapid response of telecommunication networks to environmental changes without human participation. When creating the attractor selection mechanism for network resource management, at first the so called regulatory matrix W should be defined which shows relationships between node pairs, that is, how each node pair affects each other including itself. Likely as in GRN networks, three types of influence exist, namely, activation, inhibition and no relation, corresponding to positive, negative and zero entries w ij of the regulatory matrix.
Both mentioned networks can be huge. Therefore, the respective mathematical models, formulated in terms of differential equations, also include systems of high dimensionality. The standard mathematical (qualitative and quantitative) analysis of such systems, except particular cases, seems to be difficult if it is standard. The creation of new concepts and ideas for solving this challenging problem is an actual task for mathematicians. The identification, description, systematization of attractors for systems of differential equations of high dimensionality is, therefore, an urgent task.
The classical theory of Poincaré and Bendixson exist for the two-dimensional systems. Even this theory has a number of unanswered questions, especially concerning limit cycles as nontrivial attracting sets. The three-dimensional systems have richer possibilities for the existence of attractors, other than the stable equilibria. The description and full systematization of three-dimensional attractors seems to be far from completion. Systems of the form (1), besides of their practical importance in light of the above discussion, are a very convenient object for finding and investigation of attractors of unusual nature.
In what follows we made some remarks and discuss some observations, concerning the two-dimensional and three-dimensional systems of the form (1). We provide the number and possible location of stable equilibria for typical particular cases. We consider the conditions for an equilibrium to be of the type focus. We discuss the process of bifurcation of parameters leading to the Andronov – Hopf bifurcation and emerging the isolated periodic solutions in two-dimensional and three-dimensional cases.
Boundary value problems
System (1) is a particular quasi-linear system of ordinary differential equations. These systems were intensively studied with respect to the relative boundary value problems before. The general theorem [9, 10], adapted for the case of system (1) states, that the boundary value problem (1),
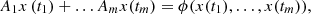 (2)where A
i
are n × n matrices with real entries, t
i
are time moments in a definite interval, φ is a continuous function of m variables, is solvable (classical continuously differentiable solution), if the function in the right hand side of (2) is bounded and the homogeneous problem,
(2)where A
i
are n × n matrices with real entries, t
i
are time moments in a definite interval, φ is a continuous function of m variables, is solvable (classical continuously differentiable solution), if the function in the right hand side of (2) is bounded and the homogeneous problem,
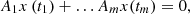 (4)where x(t) = (x
1(t), …, x
n
(t)), has only the trivial (zero) solution. This theorem is easy to apply for particular boundary conditions. Therefore the problem of existence of a solution, subject to some boundary conditions, not necessarily two-point ones, can be treated effectively. The problems on infinite intervals are specific. They often require some knowledge about the attractors of a given system.
(4)where x(t) = (x
1(t), …, x
n
(t)), has only the trivial (zero) solution. This theorem is easy to apply for particular boundary conditions. Therefore the problem of existence of a solution, subject to some boundary conditions, not necessarily two-point ones, can be treated effectively. The problems on infinite intervals are specific. They often require some knowledge about the attractors of a given system.
Consider the two-dimensional system,
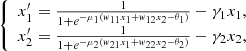 (5)together with the boundary conditions,
(5)together with the boundary conditions,
 (8)where a, A, b, B are real numbers. The homogeneous problems,
(8)where a, A, b, B are real numbers. The homogeneous problems,
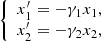 (9)
(6) and (9), (7) may have nontrivial solutions. Generally the problem (9), (6) (and/or (9), (7)) has not a solution. This is easy to see. Consider the system,
(9)
(6) and (9), (7) may have nontrivial solutions. Generally the problem (9), (6) (and/or (9), (7)) has not a solution. This is easy to see. Consider the system,
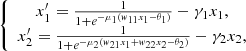 (10)together with the conditions,
(10)together with the conditions,
A solution x 1(t) is uniquely defined by the initial condition x 1(0) = A. Therefore a solution (x 1(t), x 2(t)) to the problem (10), (11) does not exist if B is not appropriate.
The above reasoning is valid also for studying the problem with periodic or antiperiodic boundary conditions. For instance, the problem (13),
 (12)is solvable for any positive T. This does not mean, however, that there always exists a closed orbit for the autonomous system, since constant solutions also are periodic, and due to the properties of a sigmoidal nonlinearities in (5) at list one critical point exists.
(12)is solvable for any positive T. This does not mean, however, that there always exists a closed orbit for the autonomous system, since constant solutions also are periodic, and due to the properties of a sigmoidal nonlinearities in (5) at list one critical point exists.
Two-dimensional cases
Consider the system,
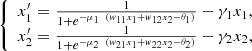 (13)that contains 10 parameters. We wish to discuss the structure of attractors for this system. We avoid the standard analysis of critical points due to multiple parameters and instead consider few variants which depend on the geometry and location of nullclines. These features depend of course on parameters but explicitly the values of parameters are not involved. It seems, that this system was not studied in such context by standard tools of a phase plane and critical points. The few related references are [1, 11].
(13)that contains 10 parameters. We wish to discuss the structure of attractors for this system. We avoid the standard analysis of critical points due to multiple parameters and instead consider few variants which depend on the geometry and location of nullclines. These features depend of course on parameters but explicitly the values of parameters are not involved. It seems, that this system was not studied in such context by standard tools of a phase plane and critical points. The few related references are [1, 11].
The regularity matrix is,
The equilibria (critical points) are to be found from the system,
The type of a (non-degenerate) critical point 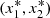 is to be detected in a standard way concerning the linearized system,
is to be detected in a standard way concerning the linearized system,
Let us list the basic facts about the system (13). The nullclines of the system (13) are defined by the relations (15). Due to properties of sigmoidal functions the nullclines are located in the strips 0 < x
1 < 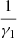 and 0 < x
2 <
and 0 < x
2 < 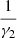 respectively. Therefore all the critical points (that are cross-points of nullclines) lie in the rectangle domain
respectively. Therefore all the critical points (that are cross-points of nullclines) lie in the rectangle domain 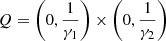 . There is at least one critical point. The inspection of the boundary of Q shows that the vector field
. There is at least one critical point. The inspection of the boundary of Q shows that the vector field 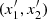 is directed inward. Any trajectory of the system (13) stays in Q eventually.
is directed inward. Any trajectory of the system (13) stays in Q eventually.
The characteristic equation for a critical point 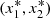 is,
is,
Up to nine critical points are possible in the system (13) [1].
Graphical analysis
Even the two-dimensional system (13) contains 10 parameters and standard analysis of all possible cases is rather long. Therefore it is convenient to treat the system graphically using the nullclines method.
Activation
Let us consider the so called activation case where w 11 = w 22 = 0, and w 12 = α > 0, w 21 = β > 0, γ 1, γ 2 are positive. The nullclines generally can be located as depicted in Figures 1–3. We set α = 1, β = 2, γ 1 = γ 2 = 1.
 |
Figure 1 One critical point, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 0.6, θ 2 = 1.0, w 11 = w 12 = w 22 = 1, w 21 = 2. |
 |
Figure 2 Two critical points, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 0.6, θ 2 = 1.5, w 11 = w 12 = w 22 = 1, w 21 = 2. |
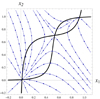 |
Figure 3 Three critical points, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 1.2, θ 2 = 1.5, w 11 = w 12 = w 22 = 1, w 21 = 2. |
In the first case there is one equilibrium and the vector field 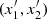 is directed towards the critical point which is a sink.
is directed towards the critical point which is a sink.
The second case is visualized in Figure 2. The nullclines are crossed at the first equilibrium and have a tangent point at the second one. The upper (simple) critical point is a sink. It can be shown [1] that the lower critical point is degenerate in the sense that one of the characteristic numbers λ is zero. It is attractive, however.
Due to S-shape of nullclines there are at most three equilibria. This is shown in Figure 3. The side equilibria are sinks and the middle one is a saddle point. If w 11 and w 22 are not zeros more critical points are possible [1].
Mixed case
Consider system (13) provided that γ 1 = γ 2 = 1, w 11 = w 22 = 0, and w 12 and w 21 have opposite signs. The nullclines together with the vector field are depicted in Figure 4. If w 12 is positive then the rotation of the vector field is in the counter clock-wise direction.
 |
Figure 4 One critical point, w 12 = −2, w 21 = 2, μ 1 = 3.5, μ 2 = 3.5, θ 1 = −0.7, θ 2 = 0.8, w 11 = w 22 = 0, w 12 = −2, w 21 = 2. |
Proposition 3.1
There is a single critical point of the type stable focus for the system (13) if w 11 = w 22 = 0 and w 12 and w 21 have opposite signs.
Proof in [1]. We get from (19) to (21) that the characteristic equation is,
The roots are 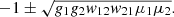 Since w
12
w
21 is negative, a unique critical point is focus.
Since w
12
w
21 is negative, a unique critical point is focus.
If w 12 is negative and w 21 positive then (Fig. 5) the rotation of vector field is in the clock-wise direction.
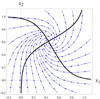 |
Figure 5 One critical point, w 12 = 2, w 21 = −2, μ 1 = μ 2 = 3.5, θ 1 = 1.3, θ 2 = −1.0, w 11 = w 22 = 0. |
Remark 3.1. There is no a closed orbit in the system (13) if w 11 = w 22 = 0. The divergence of the vector field, defined by (13), is not zero and the Bendixson criterium ([12], Ch. X, [5]) for closed orbits in the region Q is not satisfied. If w 11 and w 22 are allowed to be nonzero, the limit cycle is possible [1, 11] (see Fig. 6). Imagine that w 11 = w 22 = k > 0 The limit cycle appears as a result of Andronov – Hopf bifurcation. The unique critical point then changes the stability to instability as k increases from zero to unity and the real parts of the complex conjugate characteristic numbers λ(k) become positive passing through zero.
 |
Figure 6 One critical point, w 12 = 2, w 21 = −2, μ 1 = μ 2 = 5.0, θ 1 = 1.3, θ 2 = −0.5, w 11 = w 22 = 1. The closed trajectory (limit cycle, in black) is for x 1(0) = 0.5, x 2(0) = 0.23. |
Three-dimensional cases
Consider the three-dimensional system,
 (23)with the regulatory matrix,
(23)with the regulatory matrix,
The nullclines for the system are defined by the relations,
The critical points for the system (23) are the cross points of the nullclines. The linearized system for any critical point 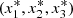 is,
is,
The nullcline analysis can work well in the three-dimensional case also. Since a critical point is the cross-point of all nullclines, the number of equilibria can be established by combination of visual observations and checking by roots finding programs. For the case under consideration the following situation is of particular interest. There exists at least one critical point in systems (23). If there are several non-attractive equilibria (saddles or unstable focuses) then an unusual behavior of solutions in the bounded domain is expected. The famous Lorenz and Rössler systems are of this kind. The Lorenz system has three critical points (a saddle and two unstable focuses) for particular values of parameters. The Rössler system has one unstable focus and a saddle. If there is exactly one critical point of this kind, then the trajectories cannot be trapped by it. We provide an example of one critical point that is unstable focus (that is, two of three characteristic numbers are complex conjugate with positive real part).
Consider the system,
The system (29) has a single critical point at (0.356279, 0.548522, 0.228589). The characteristic values for this point are λ 1 = −1.74069, λ 2,3 = 0.300343 ± 0.458758i. This critical point is not attractive. There is a periodic solution that can be drawn using the initial values (0.032, 0.1054, 0.129) (Fig. 7).
 |
Figure 7 The periodic trajectory passes through the point (0.032, 0.1054, 0.129) (in red), the unique critical point in black. |
The projections of a solution are depicted in Figures 8–10.
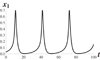 |
Figure 8 The coordinate plane (t, x 1). |
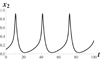 |
Figure 9 The coordinate plane (t, x 2). |
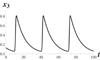 |
Figure 10 The coordinate plane (t, x 3). |
Remark 4.1. Consider the system (29) with the regulatory matrices,
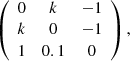 where k is a positive parameter, that changes from 0.5 to 1. For k = 0 there is a unique critical point of the type stable node, for k = 0.5 a unique critical point at (0.15226, 0.38047, 0.01324) is a stable 3D focus with the characteristic numbers λ
1 = −0.90782, λ
1,2 = −0.11609 ± 0.10694i. For k = 0.8 a unique critical point is at (0.31292, 0.53134, 0.12852) and it is unstable 3D focus with the characteristic numbers λ
1 = −1.44399, λ
2,3 = 0.1512 ± 0.361497i.
where k is a positive parameter, that changes from 0.5 to 1. For k = 0 there is a unique critical point of the type stable node, for k = 0.5 a unique critical point at (0.15226, 0.38047, 0.01324) is a stable 3D focus with the characteristic numbers λ
1 = −0.90782, λ
1,2 = −0.11609 ± 0.10694i. For k = 0.8 a unique critical point is at (0.31292, 0.53134, 0.12852) and it is unstable 3D focus with the characteristic numbers λ
1 = −1.44399, λ
2,3 = 0.1512 ± 0.361497i.
Conclusions
The nullcline method together with other tools can be effectively applied in the study of asymptotic behavior of solutions and the structure of attractors for systems of low dimensions. The conclusions made on the basis of nullcline analysis can generate the hypotheses and suggestions for higher dimensional cases. Some questions are unanswered up to now. We have examples of a system (23) with a single critical point of the type unstable focus (two complex conjugate characteristic numbers have positive real part). It is possible also to have exactly three critical points in such configuration: two unstable focuses and a saddle point.
Author contributions
The authors claim to have contributed equally and significantly in this paper. Both authors read and approved the final manuscript.
Conflict of interest
The authors declare that they have not received funds from any institution and that they have no conflict of interest.
References
- Sadyrbaev F, Ogorelova D, Samuilik I (2019), A nullclines approach to the study of 2D artificial network. Contemp Math 1, 1, 11. [Google Scholar]
- Wilson HR, Cowan JD (1972), Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12, 1, 1–24. [CrossRef] [PubMed] [Google Scholar]
- Vohradský J (2001), Neural network model of gene expression. FASEB J 15, 3, 846–854. https://doi.org/10.1096/fj.00-0361com. [CrossRef] [PubMed] [Google Scholar]
- Tušek A, Kurtanjek Ž (2012), Mathematical Modelling of Gene Regulatory Networks, Ch. 5 in: R Ganesh Naik (Ed), Applied Biological Engineering – Principles and Practice, InTech. https://doi.org/10.5772/2101 [Google Scholar]
- Crombach A, Hogeweg P (2008), Evolution of evolvability in gene regulatory networks. PLoS Comput Biol 4, 7, e1000112. https://doi.org/10.1371/journal.pcbi.1000112. [Google Scholar]
- Wuensche A (1998), Genomic regulation modeled as a network with basins of attraction. Proc Pac Symp Biocomput 3, 89–102. [Google Scholar]
- Furusawa C, Kaneko K (2008), A generic mechanism for adaptive growth rate regulation. PLoS Comput Biol 4, 1, e3. 0035–0042. https://doi.org/10.1371/journal.pcbi.0040003. [Google Scholar]
- Koizumi Y, Miyamura T, Arakawa S, Oki E, Shiomoto K, Murata M (2010), Adaptive virtual network topology control based on attractor selection. J Lightwave Technol 28, 11, 1720–1731. https://doi.org/10.1109/JLT.2010.2048412. [Google Scholar]
- Conti R (1962), Equazioni differenziali ordinarie quasilineari con condizioni lineari. Ann Mat Pura Appl 57, 49–61. [CrossRef] [Google Scholar]
- Klokov YA, Vasilyev NI (1978), Foundations of the theory of boundary value problems for ordinary differential equations, Zinatne, Riga. (in Russian). [Google Scholar]
- Sadyrbaev F (2019), Planar differential systems arising in network regulation theory. Adv Math Models Appl (Jomard Publ) 4, 1, 70–78. [Google Scholar]
- Lefschetz S (1957), Differential equations: geometric theory, Interscience Publ, New York. [Google Scholar]
Cite this article as: Brokan E & Sadyrbaev F 2020. Remarks on GRN-type systems. 4open, 3, 8
All Figures
 |
Figure 1 One critical point, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 0.6, θ 2 = 1.0, w 11 = w 12 = w 22 = 1, w 21 = 2. |
| In the text | |
 |
Figure 2 Two critical points, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 0.6, θ 2 = 1.5, w 11 = w 12 = w 22 = 1, w 21 = 2. |
| In the text | |
 |
Figure 3 Three critical points, μ 1 = 3.5, μ 2 = 3.2, θ 1 = 1.2, θ 2 = 1.5, w 11 = w 12 = w 22 = 1, w 21 = 2. |
| In the text | |
 |
Figure 4 One critical point, w 12 = −2, w 21 = 2, μ 1 = 3.5, μ 2 = 3.5, θ 1 = −0.7, θ 2 = 0.8, w 11 = w 22 = 0, w 12 = −2, w 21 = 2. |
| In the text | |
 |
Figure 5 One critical point, w 12 = 2, w 21 = −2, μ 1 = μ 2 = 3.5, θ 1 = 1.3, θ 2 = −1.0, w 11 = w 22 = 0. |
| In the text | |
 |
Figure 6 One critical point, w 12 = 2, w 21 = −2, μ 1 = μ 2 = 5.0, θ 1 = 1.3, θ 2 = −0.5, w 11 = w 22 = 1. The closed trajectory (limit cycle, in black) is for x 1(0) = 0.5, x 2(0) = 0.23. |
| In the text | |
 |
Figure 7 The periodic trajectory passes through the point (0.032, 0.1054, 0.129) (in red), the unique critical point in black. |
| In the text | |
 |
Figure 8 The coordinate plane (t, x 1). |
| In the text | |
 |
Figure 9 The coordinate plane (t, x 2). |
| In the text | |
 |
Figure 10 The coordinate plane (t, x 3). |
| In the text | |


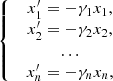


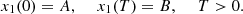
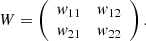
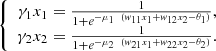
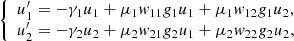
![$$ {g}_1=\frac{{e}^{-{\mu }_1({w}_{11}{x}_1^{\mathrm{*}}+{w}_{12}{x}_2^{\mathrm{*}}-{\theta }_1)}}{[1+{e}^{-{\mu }_1({w}_{11}{x}_1^{\mathrm{*}}+{w}_{12}{x}_2^{\mathrm{*}}-{\theta }_1)}{]}^2}, $$](/articles/fopen/full_html/2020/01/fopen200009/fopen200009-eq20.gif)
![$$ {g}_2=\frac{{e}^{-{\mu }_2({w}_{21}{x}_1^{\mathrm{*}}+{w}_{22}{x}_2^{\mathrm{*}}-{\theta }_2)}}{[1+{e}^{-{\mu }_2({w}_{21}{x}_1^{\mathrm{*}}+{w}_{22}{x}_2^{\mathrm{*}}-{\theta }_2)}{]}^2}. $$](/articles/fopen/full_html/2020/01/fopen200009/fopen200009-eq21.gif)
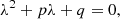
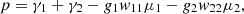
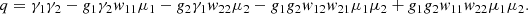
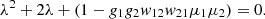


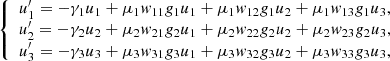
![$$ {g}_1=\frac{{e}^{-{\mu }_1({w}_{11}{x}_1^{\mathrm{*}}+{w}_{12}{x}_2^{\mathrm{*}}+{w}_{13}{x}_3^{\mathrm{*}}-{\theta }_1)}}{[1+{e}^{-{\mu }_1({w}_{11}{x}_1^{\mathrm{*}}+{w}_{12}{x}_2^{\mathrm{*}}+{w}_{13}{x}_3^{\mathrm{*}}-{\theta }_1)}{]}^2}, $$](/articles/fopen/full_html/2020/01/fopen200009/fopen200009-eq38.gif)
![$$ {g}_2=\frac{{e}^{-{\mu }_2({w}_{21}{x}_1^{\mathrm{*}}+{w}_{22}{x}_2^{\mathrm{*}}+{w}_{23}{x}_3^{\mathrm{*}}-{\theta }_2)}}{[1+{e}^{-{\mu }_2({w}_{21}{x}_1^{\mathrm{*}}+{w}_{22}{x}_2^{\mathrm{*}}+{w}_{23}{x}_3^{\mathrm{*}}-{\theta }_2)}{]}^2}, $$](/articles/fopen/full_html/2020/01/fopen200009/fopen200009-eq39.gif)
![$$ {g}_3=\frac{{e}^{-{\mu }_3({w}_{31}{x}_1^{\mathrm{*}}+{w}_{32}{x}_2^{\mathrm{*}}+{w}_{33}{x}_3^{\mathrm{*}}-{\theta }_3)}}{[1+{e}^{-{\mu }_3({w}_{31}{x}_1^{\mathrm{*}}+{w}_{32}{x}_2^{\mathrm{*}}+{w}_{33}{x}_3^{\mathrm{*}}-{\theta }_3)}{]}^2}. $$](/articles/fopen/full_html/2020/01/fopen200009/fopen200009-eq40.gif)