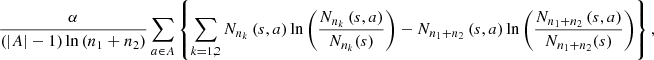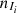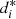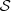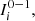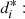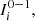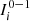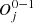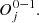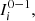| Issue |
4open
Volume 3, 2020
|
|
|---|---|---|
| Article Number | 9 | |
| Number of page(s) | 11 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2020010 | |
| Published online | 21 August 2020 | |
Research Article
Risk of fraud classification
1
Department of Statistics, University of Campinas, Sergio Buarque de Holanda, 651, CEP: 13083-859, Campinas, SP, Brazil
2
CPFL, Rod. Eng. Miguel Noel Nascentes Burnier, 1755 – Chácara Primavera, CEP: 13088-900, Campinas, SP, Brazil
* Corresponding author: thainass@outlook.com
Received:
17
March
2020
Accepted:
19
July
2020
In this article, we define consumers’ profiles of electricity who commit fraud. We also compare these profiles with users’ profiles not classified as fraudsters in order to determine which of these clients should receive an inspection. We present a statistically consistent method to classify clients/users as fraudsters or not, according to the profiles of previously identified fraudsters. We show that it is possible to use several characteristics to inspect the classification of fraud; those aspects are represented by the coding performed in the observed series of clients/users. In this way, several encodings can be used, and the client risk can be constructed to integrate complementary aspects. We show that the classification method has success rates that exceed 77%, which allows us to infer confidence in the methodology.
Key words: Bayesian Information Criterion / Partition Markov Models / Metric in Markov Processes
© J.E. García et al., Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
This article is oriented to the solution of a real problem through stochastic processes techniques. Institutions/companies collect information from users/customers to determine their profiles on consumption practices, preferences, and socio-economic features, among other aspects. That is, in general terms, they seek to establish behavioral profiles. This knowledge can facilitate the placement of products or the rapid adaptation of an institution to meet the needs of its users. The coding of the information allows defining these profiles, which constitute representations of the behavior. Such representations provide information to institutions and companies to form teams that can dedicate themselves to optimizing the relationship with these groups characterized by specific profiles. Those profiles are defined using the knowledge about the performance of certain sequences (user history coding). The problem of determining groups and profiles can be approached from discrete stochastic processes tools, since, in this area, there are powerful tools to deal with the problem, see [1], [2] and [3]. The sequences resulting from the coding of user/customer data can be identified as samples coming from discrete stochastic processes. In this article, we develop a method to classify sequences, according to k I previously determined profiles. Then the k I profiles are compared with the performance of other unclassified sequences (or group of). For this purpose, it is necessary to have some tools, (A) a tool that is capable of (i) discriminating between processes by samples from them, (ii) determining whether the processes represented by their samples are from the same stochastic law, (B) a tool that allows drawing a stochastic profile of the behavior of a process based on a series of sequences (group) that are judged to come from the same process. As a consequence of addressing this issue, in this article, we address the problem of classifying clients as fraudsters. We employ a set of real data on electricity consumption. The proposal is to attribute to each classified client, a risk related to the similarity that its series of consumption shows with some group of fraudulent clients, identified through (A)–(B).
This article is organized as follows. Section 2 addresses the theoretical foundations and classification strategy. Section 3 describes the data, the coding, and the calculation of the risk to customers. Also, in this section, the notion of fraud customers and the groups found in the database are discussed. The conclusions and considerations are given in Section 4.
Theoretical background
We begin this section by introducing the notation used in the formalization of stochastic tools. Let (Z
t
)
t
be a discrete time Markov chain of order o (o < ∞) with finite alphabet A. Let us call  = A
o
the state space and denote the string a
m
a
m+1…a
n
by
= A
o
the state space and denote the string a
m
a
m+1…a
n
by  where a
i
∈ A, m ≤ i≤ n. For each a ∈ A and s ∈
where a
i
∈ A, m ≤ i≤ n. For each a ∈ A and s ∈ 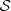 define the transition probability
define the transition probability 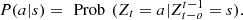 In a given sample
In a given sample 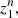 coming from the stochastic process, the number of occurrences of s is denoted by N
n
(s) and the number of occurrences of s followed by a is denoted by N
n
(s, a). In this way,
coming from the stochastic process, the number of occurrences of s is denoted by N
n
(s) and the number of occurrences of s followed by a is denoted by N
n
(s, a). In this way, 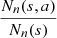 is the maximum likelihood estimator of P(a|s). Consider now, two Markov chains (Z
1,t
)
t
and (Z
2,t
)
t
, of order o, disposed on the finite alphabet A with state space
is the maximum likelihood estimator of P(a|s). Consider now, two Markov chains (Z
1,t
)
t
and (Z
2,t
)
t
, of order o, disposed on the finite alphabet A with state space  . Given s ∈
. Given s ∈  denote by {P(a|s)}
a∈A
and {Q(a|s)}
a∈A
the sets of transition probabilities of (Z
1,t
)
t
and (Z
2,t
)
t
, respectively. Consider now the local metric d
s
introduced by [1], note that d
s
is a metric in
denote by {P(a|s)}
a∈A
and {Q(a|s)}
a∈A
the sets of transition probabilities of (Z
1,t
)
t
and (Z
2,t
)
t
, respectively. Consider now the local metric d
s
introduced by [1], note that d
s
is a metric in  (not negative, symmetric and follows triangular inequality) and it allows defining a global notion (in
(not negative, symmetric and follows triangular inequality) and it allows defining a global notion (in 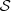 ) of similarity between sequences.
) of similarity between sequences.
Definition 1
Consider two Markov chains (Z
1,t
)
t
and (Z
2,t
)
t
of order o, with finite alphabet A, state space 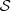 = A
o
and independent samples
= A
o
and independent samples 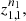
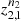 respectively. Then, set
respectively. Then, set
-
for each s ∈


 , where
, where  and
and  are given as usual, computed from the samples
are given as usual, computed from the samples  and
and  respectively. Moreover, α is a real and positive value.
respectively. Moreover, α is a real and positive value.
The Definition 1 introduces two notions of proximity between sequences, i. is local, ii. is global; both are statistically consistent, since, by increasing the min{n 1, n 2}, grows their capacity to detect discrepancies (when the underlying laws are different) and similarities (when the underlying laws are the same). To decide if the sequences follow the same law, is only necessary to check that d s < 1. This threshold is derived from the Bayesian Information Criterion (BIC), see [1]. In the application, we use α = 2, with this value, we recover the usual expression of the BIC, given by [4].
The next notion (Partition Markov Model-PMM) allows postulating a parsimonious model for a Markov process, aiming at the identification of states in the state space, which have in common their transition probabilities. Through this model we build the stochastic profiles.
Definition 2
Let (Z t ) t be a discrete time Markov chain of order o on a finite alphabet A, with state space S = A o ,
-
s, r ∈ S are equivalent if P(a|s) = P(a|r) ∀ a ∈ A.
-
(Z t ) t is a Markov chain with partition
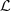 = {L
1, L
2, …,
= {L
1, L
2, …,  } if this partition is the one defined by the equivalence introduced by item i.
} if this partition is the one defined by the equivalence introduced by item i.
The model given by Definition 2 was introduced in reference [2] as well as the strategy for its consistent estimation that is also based on a metric defined on the state space and based on the BIC. The parameters to be estimated are (a) the partition  , (b) the transition probabilities of each part L to any element of A, P(⋅|L) = ∑
s∈S
P(⋅|s). Given a sample of
, (b) the transition probabilities of each part L to any element of A, P(⋅|L) = ∑
s∈S
P(⋅|s). Given a sample of 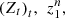 according to [2] the partition is estimated by means of
according to [2] the partition is estimated by means of 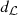 given by Definition 3.
given by Definition 3.
Definition 3
Let (Z
t
)
t
be a Markov chain of order o, with finite alphabet A and state space S = A
o,  a sample of the process and let
a sample of the process and let 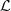 = {L
1, L
2, …,
= {L
1, L
2, …, 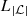 } be a partition of S such that for all s, r ∈ L, P(⋅|s) = P(⋅|r). Then, set
} be a partition of S such that for all s, r ∈ L, P(⋅|s) = P(⋅|r). Then, set  (i,j) between parts L
i
and L
j
as
(i,j) between parts L
i
and L
j
as
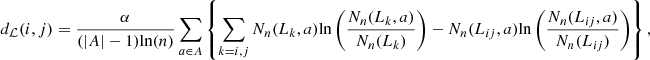 with N
n
(L) = ∑
s∈L
N
n
(s), N
n(L, a) = ∑
s∈L
N
n
(s, a), for a ∈ A, L ∈
with N
n
(L) = ∑
s∈L
N
n
(s), N
n(L, a) = ∑
s∈L
N
n
(s, a), for a ∈ A, L ∈  , L
ij
= L
i
∪ L
j
, N
n
(L
ij
) = N
n
(L
i
) + N
n
(L
j
) and N
n
(L
ij
, a) = N
n
(L
i
, a) + N
n
(L
j
, a), for a ∈ A. α a real and positive value.
, L
ij
= L
i
∪ L
j
, N
n
(L
ij
) = N
n
(L
i
) + N
n
(L
j
) and N
n
(L
ij
, a) = N
n
(L
i
, a) + N
n
(L
j
, a), for a ∈ A. α a real and positive value.
The metric  is designed to build a structure in the state space, identifying equivalent states, it is applied for example in an initial set consisting of the entire state space S, and whenever
is designed to build a structure in the state space, identifying equivalent states, it is applied for example in an initial set consisting of the entire state space S, and whenever  (i, j) < 1 the elements L
i
and L
j
must be in the same part (see properties of
(i, j) < 1 the elements L
i
and L
j
must be in the same part (see properties of  in [2]). For each part L of
in [2]). For each part L of  (estimated partition) the transition probability is estimated by
(estimated partition) the transition probability is estimated by  Note that all equivalent states are used to estimate these probabilities, in this way, an economy is produced in the total number of probabilities to be estimated.
Note that all equivalent states are used to estimate these probabilities, in this way, an economy is produced in the total number of probabilities to be estimated.
In the next subsection we show how integrate the tools presented here to build sequence groups (clusters) with the same stochastic law. We also explain how to define the stochastic profile of each cluster.
Clusters of sequences and partition by cluster
Given a collection of p sequences 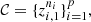 under the assumptions of Definition 1, the notion dmax ii – Definition 1 is used to define clusters in
under the assumptions of Definition 1, the notion dmax ii – Definition 1 is used to define clusters in  . We introduce an algorithm that shows how this is done.
. We introduce an algorithm that shows how this is done.
Algorithm 1
• Input

1. M = 
2. M = {m 1, …, m |M|},
3. (i *, j *) = argmin{dmax(m i , m j ), i ≠j, i, j ∈ {1, 2, …, |M|}}
* if  ,
,  with
with  and go back to 2,
and go back to 2,
* otherwise the procedure ends.
• Output (clusters of  ) M = {C
1, …, C
k
}
) M = {C
1, …, C
k
}
That is, the initial M is composed by all the separate sequences and the final M corresponds to the groups of sequences or clusters. Note that given two different sequences  ∈
∈  the occurrence of each s ∈
the occurrence of each s ∈  is recorded by
is recorded by  and
and  respectively, and the occurrence of s followed by a ∈ A is computed by
respectively, and the occurrence of s followed by a ∈ A is computed by  and
and  . Already, when defining the new unit
. Already, when defining the new unit  (after verifying
(after verifying  ) the count of the ocurrences of s, is given by
) the count of the ocurrences of s, is given by  and if a ∈ A, the ocurrences of s followed by a is
and if a ∈ A, the ocurrences of s followed by a is 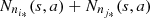 . That is, in the case of
. That is, in the case of 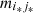 both sequences,
both sequences,  and
and  , contribute to the count attributed to
, contribute to the count attributed to  .
.
Once the proximity between sequences is determined in order to build the clusters {C 1, …, C k } and for each cluster we can build a PMM, representing the cluster. In addition, it is possible to quantify the dissimilarity between clusters using the notion dmax. Suppose the cluster i is C i and it is composed by m i independent sequences,
 the sample size related to C
i
is
the sample size related to C
i
is  . For each s ∈
. For each s ∈ 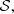 compute the ocurrences of s in C
i
as
compute the ocurrences of s in C
i
as
 (1)and the ocurrences of s followed by a as
(1)and the ocurrences of s followed by a as
The following remark shows how to determine the stochastic profile of each cluster.
Remark 1
If we replace in Definition 3 the sample size n by  and applying the Algorithm 1, substituting (i)
and applying the Algorithm 1, substituting (i)  by S = A
o, (ii) dmax by
by S = A
o, (ii) dmax by 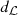 , the Output of the algorithm will be the partition
, the Output of the algorithm will be the partition 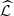 i
of S, related to the cluster C
i
.
i
of S, related to the cluster C
i
.
The following remark shows how to measure the similarity between two clusters.
Remark 2
To establish the dissimilarity between the clusters C
1 and C
2 (since by construccion those are different) we use the Definition 1 – ii. In the calculation of i-def 2.1, we replace 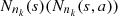 by equation (1) ((2)), with i = k. We replace also
by equation (1) ((2)), with i = k. We replace also  by N(C
1
, s) + N(C
2
, s) and
by N(C
1
, s) + N(C
2
, s) and  by N(C
1
, (s, a)) + N(C
2
, (s, a)). Using those ocurrences we can compute the dissimilarity between the clusters.
by N(C
1
, (s, a)) + N(C
2
, (s, a)). Using those ocurrences we can compute the dissimilarity between the clusters.
The next section is intended to apply the concepts detailed here as well as the strategies presented to real data.
Risk through Discretized Information
Data and structure of the analises
In Table 1, we describe the data inspected in this paper. The data correspond to serial records of energy consumption of clients of a company of power supply (CPFL) during the period: January 2011 to June 2019. We have two types of records, Irregular classified by specialists in fraud and Other which are not be classified as Irregular. That is, irregular cases have already been classified since they were identified by the fraud detection system of the company. The other cases appear to be normal but could have been disregarded by the system used in fraud detection.
Biphasic clients reported by CPFL, period: January, 2011 to June, 2019.
The monthly energy consumption sequence of each client i,  is discretized in order to identify it with a sample of a Markov stochastic process (Z
i,t
)
t
, of finite order o in the discrete and finite alphabet A, for i = 1, …, 8381. The first inspection to be carried out seeks to identify clusters in Irregular clients, this classification could point to specific fraud practices. So we determine
is discretized in order to identify it with a sample of a Markov stochastic process (Z
i,t
)
t
, of finite order o in the discrete and finite alphabet A, for i = 1, …, 8381. The first inspection to be carried out seeks to identify clusters in Irregular clients, this classification could point to specific fraud practices. So we determine 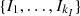 clusters of irregular clients, applying the Algorithm 1 in the set of irregular clients. For the group Other, we also determine the clusters, say
clusters of irregular clients, applying the Algorithm 1 in the set of irregular clients. For the group Other, we also determine the clusters, say  (by applying Algorithm 1 in Other). So, we can classify customers into consumer practices. Once the Irregular clusters have been constructed, it is possible to quantify the dissimilarity between them, this is done by means of dmax as described in the previous section (see Remark 2), computing dmax(I
i
, I
j
), i ≠ j, i, j ∈ {1, 2, …, k
I
}. In a second instance, we compare the behavior of the O
l
, l = 1, …, k
O
clusters with the irregular ones, computing dmax(I
i
, O
l
), i ∈ {1, …, k
I
}, l ∈ {1, …, k
O
}. We do this comparison in order to identify which could be considered as indistinguishable from some irregular cluster, this happens when dmax(I
i
, O
l
) < 1. Such a comparison generates a risk index in the class
(by applying Algorithm 1 in Other). So, we can classify customers into consumer practices. Once the Irregular clusters have been constructed, it is possible to quantify the dissimilarity between them, this is done by means of dmax as described in the previous section (see Remark 2), computing dmax(I
i
, I
j
), i ≠ j, i, j ∈ {1, 2, …, k
I
}. In a second instance, we compare the behavior of the O
l
, l = 1, …, k
O
clusters with the irregular ones, computing dmax(I
i
, O
l
), i ∈ {1, …, k
I
}, l ∈ {1, …, k
O
}. We do this comparison in order to identify which could be considered as indistinguishable from some irregular cluster, this happens when dmax(I
i
, O
l
) < 1. Such a comparison generates a risk index in the class 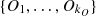 , as to guide the inspection of the company in that class. For each client
, as to guide the inspection of the company in that class. For each client  we define:
we define:
In this way, the values obtained from equation (3) reported for the clients in the class Other (Tab. 1) are  By construction for the client υ in Other, ∃! i
υ
∈ {1, …, k
O
} such that
By construction for the client υ in Other, ∃! i
υ
∈ {1, …, k
O
} such that  allowing the good definition of equation (3). Denote by a
v
(1), a
v
(2), …, a
v
(7828) the ordered values in an increasing way. Thus, the client that receives the value a
v
(1) is the one with the highest risk and the one that receives the value a
v
(7828) is the client with the lowest risk, taking into account that the threshold equal to 1 allows us to pay attention only in the clients whose values fall in [0, 1). Figure 1 illustrates the situation.
allowing the good definition of equation (3). Denote by a
v
(1), a
v
(2), …, a
v
(7828) the ordered values in an increasing way. Thus, the client that receives the value a
v
(1) is the one with the highest risk and the one that receives the value a
v
(7828) is the client with the lowest risk, taking into account that the threshold equal to 1 allows us to pay attention only in the clients whose values fall in [0, 1). Figure 1 illustrates the situation.
 |
Figure 1 Scheme of the organization of the ordered values |
Results
We compare the series of consumption through a discretization that considers four possible states, and reports the performance of the series in relation to the magnitude of the consumption in the last measurement (at time t) when compared with the two previous measurements (times t − 1 and t − 2). For each client i with 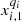 consumption series define the sample
consumption series define the sample 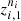 of the discrete process (Z
i,t
)
t
as
of the discrete process (Z
i,t
)
t
as
Then, A = {1, 2, 3, 4} and |A| = 4. In the set of sequences, the smaller one has a sample size equal to 39, the indicated order o follows the rule: o < log4(39) = 2.643, then o = 2. The application of the Algorithm 1 in the Irregular group generates k
I
= 12 clusters. Table 2 exposes the maximum value of dmax reported by the algorithm, inside each cluster, denoted by  . These results measure the homogeneity within each irregular cluster. Lower values of
. These results measure the homogeneity within each irregular cluster. Lower values of 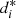 indicate greater homogeneity, and values of
indicate greater homogeneity, and values of 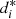 close to 1 indicate greater heterogeneity.
close to 1 indicate greater heterogeneity.
After identifying 12 Irregular clusters, we can explore the dissimilarity between them computing the values of dmax between the clusters (see Remark 2). Table 3 shows the results.
In a stochastic way, the table quantifies the differences in fraud practices classified by the company. With the purpose of exploring the dynamics of each irregular cluster, we fit a PMM model for each cluster. This leads us to describe the meaning of each possible state for the (Z
i,t
)
t
process. In Table 4, we report the relation of the states s ∈ 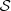 with the consumption. Each possible state is composed of the concatenation of a and b in A, so the state is ab. By construction, the states relate the magnitudes of the energy consumption at times t − 3, t − 2, t − 1 and t, thus, for example, the state ab = 13 means {X
t
≥ X
t−1 & X
t
≥ X
t−2} (associated with b = 3) and {X
t−1 < X
t−2 & X
t−1 < X
t−3} (associated with a = 1). Note that some combinations are not allowed by construction, those are 12, 22, 33, 43 (see Tab. 5).
with the consumption. Each possible state is composed of the concatenation of a and b in A, so the state is ab. By construction, the states relate the magnitudes of the energy consumption at times t − 3, t − 2, t − 1 and t, thus, for example, the state ab = 13 means {X
t
≥ X
t−1 & X
t
≥ X
t−2} (associated with b = 3) and {X
t−1 < X
t−2 & X
t−1 < X
t−3} (associated with a = 1). Note that some combinations are not allowed by construction, those are 12, 22, 33, 43 (see Tab. 5).
Note that the states described in Table 4 indicate a decreasing/increasing trajectory ending, and this behavior is reflected in the partitions generated for each irregular cluster (see Tabs. 6 and 7), with only two possible exceptions, for states that allow consumption maintenance. Consider two large groups: those of increasing final trajectories (a) 13, 14, 23, 24, 34, 44 (including increasing/maintenance) and those of decreasing final trajectories (b) 11, 21, 31, 32, 41, 42. We see that all models (except in two situations) have separated the states into those two large classes. That is, in each part of each model we only find states of one type. For example, let’s take I 11, it is composed by 5 parts, 2 parts composed by states with a decreasing trajectory ending: L 1 = {11, 31, 42, 21, 32} and L 5 = {41} and, 3 parts composed by states with increasing trajectory ending: L 2 = {13, 23}, L 3 = {14, 24}, L 4 = {34, 44}. The exceptions are for I 1, the part L 4 = {31, 42, 34}, where 31 and 42 have decreasing endings and 34 allows increasing ending, and for I 3 the part L 3 = {21, 23} where 21 has decreasing ending and 23 allows increasing ending.
From the magnitudes of the estimated probabilities (Tabs. 6 and 7) we see that the clusters show two preferences (in bold), for state 1, cases I 1, I 2, I 3, I 4, I 7, I 9, I 12 and for state 4 the remaining cases, I 5, I 6, I 8, I 10, I 11. State 1 indicates decrease in consumption at time t in relation to the other previous instances t − 1 and t − 2 and 4 indicates increase/maintenance of consumption at time t in relation to the other previous instances t − 1 and t – 2. Moreover, for all cases I i , i = 1, …, 12 the first two elections (the two highest probabilities) fall in states 1 or 4. Note that when the preference is the state 1, the past states (elements of the parts) end in 1 or 2, that is to say, that according to the classification given in Table 4, the process was already in a decreasing final trajectory (except I 3). When the preference is state 4, the past states (elements in the parts) end in 3 or 4, that is, according to the classification (Tab. 4), the process was in maintenance or increasing trajectory.
The group Other is divided by the Algorithm 1 (coding Z i,t – equation (4)) in 391 clusters, so k O = 391. As the purpose of this paper is to identify those customers in the Other category that resemble an irregular cluster, we proceed to measure this similarity. For each I i we calculate dmax between such irregular cluster and the clusters O j , j = 1, …, k O . Table 8 summarizes the obtained values.
In Table 9, we report which O j clusters behave as irregular. The lower the value of dmax on the right, the higher the risk of group O j as it becomes indistinguishable from an irregular.
We note that there are 63 clients that deserve a detailed inspection, since their risks are pronounced (dmax values below 0.7). And certainly, the priority is for the 36 with approximately zero dmax.
As set forth in Table 4, Irregular processes define their minimum units, parts of the partitions, according to the types of final trajectories (a) increasing/maintenance final trajectories and (b) decreasing final trajectories, which leads us to inspect the consumption series via a representation showing that trend. The following subsection is intended for this purpose.
Increasing and decreasing movements
Based on the findings we introduce a complementary coding that allows us another perspective of the study. For that, we consider two movements in the consumption series. For each client i with series  define the sample
define the sample  of the discrete process (Y
i,t
)
t
as
of the discrete process (Y
i,t
)
t
as
Then, A = {0, 1} and |A| = 2. We adopt the memory o = 2 in order to facilitate the interpretation in concordance with the previous inspection. See the meaning of the states of the process (Y i,t ) t in Table 10.
In Table 11 we show the k
I
= 22 clusters defined by the Algorithm 1 in the Irregular class (Tab. 1),  , i = 1, …, 22 clusters derived from the codification Y
i,t
– see equation (5).
, i = 1, …, 22 clusters derived from the codification Y
i,t
– see equation (5).
We see that in relation to the irregular clusters via the Z
i,t
encoding, the Y
i,t
encoding almost doubles the irregularity modalities. While the Table 2 reports only 3 in 12 (25%) cases with d* < 0.5, Table 11 reports 12 in 22 (55%) cases with d* < 0.5, which explains the increase in the number of groups reported in Table 11. In the Appendix, Tables 16 and 17, we report the PMM for each Irregular cluster derived from the codification (Y
i,t
)
t
. We report 14 models with only two parts, 7 with 3 parts and 1 model with 4 parts. States 00 and 11, which reiterate a trend of consecutive decrease in energy consumption or consecutive increase/maintenance are found in separate parts in all models except in four cases:  , i = 11, 12, 13, 20.
, i = 11, 12, 13, 20.
The group Other, under the representation Y
i,t
equation (5) is divided by Algorithm 1 in 128 clusters,  with k
O
= 128. That is, we obtain an increase the profiles of the Irregular clusters, from 12 to 22, and a decrease of the clusters in the class Other, from 391 to 128.
with k
O
= 128. That is, we obtain an increase the profiles of the Irregular clusters, from 12 to 22, and a decrease of the clusters in the class Other, from 391 to 128.
For each  we calculate the dmax between such irregular cluster and the clusters
we calculate the dmax between such irregular cluster and the clusters  , j = 1, …, k
O
, Table 12 shows the results. According to coding 0−1, the only cluster
, j = 1, …, k
O
, Table 12 shows the results. According to coding 0−1, the only cluster  that is not associated with any element of the class Other (see Tab. 1) is the
that is not associated with any element of the class Other (see Tab. 1) is the  which has 68 clients. We must not lose sight of the fact that the risk increases when obtaining values of dmax close to zero, and only those cases need to be identified. All criteria are asymptotic so, they should be considered with caution, that is to say that, cases with dmax near to the threshold 1 can wrongly point cases that are regular one.
which has 68 clients. We must not lose sight of the fact that the risk increases when obtaining values of dmax close to zero, and only those cases need to be identified. All criteria are asymptotic so, they should be considered with caution, that is to say that, cases with dmax near to the threshold 1 can wrongly point cases that are regular one.
As we can see, from the results reported in Table 13, we see that in relation to the meaning given by the Y i,t coding (see Tab. 10), the total number of cases in the class Other that can be identified with irregular clusters, increases considerably. These results could indicate the relevance of the memory of the process, since we see that coding 1–4 reaches a greater past in comparison with coding 0−1 (compare Tabs. 4 and 10), being able to separate in a more realistic way the class Other of the class Irregular.
As the discretization caused by equations (4) and (5) lead us to simplifications of the original information, we proceed to consider both for the classification of clients. In the next subsection we take both codifications into account and propose a strategy for the inspection of potentially fraudulent customers.
Risk of clients from two codifications
It is always wise to consider that the representations given by the (Z
i,t
)
t
and (Y
i,t
)
t
processes (see Eqs. (4) and (5)) only capture certain aspects of the original consumption series. As those reveal complementary information, in this subsection we consider both to guide the decision-making process in the search for undetected frauds. We introduce a function that allows a risk classification integrating both codifications, generated by equation (3). For each client 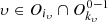 we compute:
we compute:
Note that by construction, for each client υ in Other, ∃! i
υ
∈ {1, …, 391} such that  and ∃! k
υ
∈ {1, …, 128} such that
and ∃! k
υ
∈ {1, …, 128} such that  , then we obtain a good definition of equations (6) and (7). a
υ
and b
υ
represent marginal risks of client υ, since, a
υ
depends on Z
i,t
– see equation (4) and b
υ
depends on Y
i,t
– see equation (5). Even more, we can include in the risk definition process other representations, according to the information provided by the inspeccion. In Table 14 we report the number of cases, in the class Other (see Tab. 1), by risk bands.
, then we obtain a good definition of equations (6) and (7). a
υ
and b
υ
represent marginal risks of client υ, since, a
υ
depends on Z
i,t
– see equation (4) and b
υ
depends on Y
i,t
– see equation (5). Even more, we can include in the risk definition process other representations, according to the information provided by the inspeccion. In Table 14 we report the number of cases, in the class Other (see Tab. 1), by risk bands.
If we consider as low risk those clients with dmax near to 1 or more, there are 79 risk cases that should be inspected, cases inside the set [0, 0.9] × [0, 0.9] (in bold letter – Tab. 14). As exemplified in Table 14, various representations of the original information can be integrated into the definition of a client’s risk, in this case, we have adopted two, which have revealed the need to first inspect 79 clients, according to both representations. If the cases indicated for inspection are many, according to the availability of the company, customer selection criteria such as the one described in [5] may be applied. Reference [5] shows that through a robust criterion, it is possible to select a representative client of the cluster that could be first inspected.
In the following subsection, we analyze the ability to detecting fraud, of the proposed strategy (see Eq. (3)), under each type of discretization (4) and (5).
Assertiveness of classification
We reserve this subsection to identify the predictive capacity of the classification given by Algorithm 1. What interests us is the quality of classification of Irregular customers, as these have gone through rigorous inspection processes, being defined as fraud. The database of our inspection is given in Table 1; for this, we proceed as follows. Consider the clusters defined by Algorithm 1 in the Irregular class: 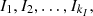 (i) randomly select s% of irregular customers, say
(i) randomly select s% of irregular customers, say  ; (ii) apply Algorithm 1 in the Irregular class (without the clients selected in (i)) and denote the clusters as
; (ii) apply Algorithm 1 in the Irregular class (without the clients selected in (i)) and denote the clusters as  (iii) For each element
(iii) For each element  find the cluster
find the cluster 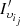 such that
such that 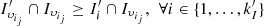 , (iv.a) compute
, (iv.a) compute 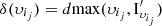 and (iv.b) record
and (iv.b) record 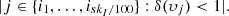
Note that the cluster 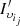 such that (iii) is verified can be considered as the most indicated cluster for the client
such that (iii) is verified can be considered as the most indicated cluster for the client  , since the client
, since the client 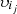 is a member of
is a member of 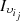 and the sets
and the sets 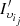 and
and 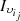 share the largest number of customers.
share the largest number of customers.
Note that under both discretizations, the average percentage of successes is greater than 77% and, the minimum percentages exceed 65%, in the three settings by discretization, see Table 15.
4 Conclusion
In practical terms, this article deals with the capacity that discretizations have to extract relevant information contained in observations in series. Such discretizations make it possible to use and adapt tools from discrete stochastic processes. Through the metric – Definition 1 (see [1]), it is possible to measure the similarity/discrepancy between samples of discrete stochastic processes. Such a metric is statistically consistent for establishing the similarity/discrepancy. Based on the metric, in this article is proposed Algorithm 1 that defines clusters of samples, where each cluster contains those sequences that respond to the same stochastic law. From the previously demonstrated properties, see [1], the clusters are then assembled consistently and represent different profiles associated with the sequences inside. To identify how these profiles operate, we use the Partition Markov Models – Definition 2 – [2], which by means of a metric – Definition 3 is consistently estimated using the sequences located in the cluster. We generate a model for each cluster, which gives the minimal representation of the state space (partition) and the transition probabilities for any element of the alphabet. Based on all these elements, we deal with a real problem where there are sequences of observations of energy consumption of two groups (i) Irregular, (ii) Other – see Table 1. We define two types of discretization ((4) and (5)) through them we proceed to identify the clusters of (i) that group similar consumption practices, we do the same with (ii). Through Partition Markov Models, we represent the stochastic profile of each cluster of (i) – see Remark 1. We identify which clusters of (ii) are confused with the clusters of (i) – see Remark 2, which allows us to point out the cases in (ii) that deserve inspection. The classification’s rates of success given by the procedure are high, as shown in the study of Section 3.5, and on average, these exceed 77%. This whole procedure allows us to establish risk indicators for (ii) and also an order that indicates the most and least serious cases. We see then that, by means of two discretizations it is possible to point cases to be reviewed, according to the magnitudes of the notion (3), our results – Table 14 – states that 79 cases should go through revision, according to (6) and (7). For additional details, see [6].
Acknowledgments
The authors Hugo Helito da Silva and T. Soares Silva gratefully acknowledge the financial support provided by ANEEL R&D Program under grant PD-00063-3037/2018, developed by CPFL Energia. Also, the authors wish to thank the Editor-led peer review process and the reviewers which generated many helpful comments and suggestions on an earlier draft of this paper.
Appendix
References
- García Jesús E, Gholizadeh R, González-López VA (2018), A BIC-based consistent metric between Markovian processes. Appl Stoch Models Bus Ind 34, 6, 868–878. [Google Scholar]
- García Jesús E, González-López VA (2017), Consistent estimation of Partition Markov Models. Entropy 19, 4, 160. [CrossRef] [Google Scholar]
- Cordeiro MTA, García Jesús E, González-López VA, Londoño SLM (2019), Classification of autochthonous dengue virus type 1 strains circulating in Japan in 2014. 4open 2, 20. [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz G (1978), Estimating the dimension of a model. Ann Stat 6, 2, 461–464. [Google Scholar]
- Fernández M, García Jesús E, Gholizadeh R, González-López VA (2019), Sample selection procedure in daily trading volume processes. Math Meth Appl Sci 43, 7537–7549. https://doi.org/10.1002/mma.5705. [CrossRef] [Google Scholar]
- Soares Silva T (2020), Similaridades entre Processos de Markov (unpublished master’s thesis). [Google Scholar]
Cite this article as: García JE, González-López VA, da Silva HH & Silva TS 2020. Risk of fraud classification. 4open, 3, 9
All Tables
All Figures
 |
Figure 1 Scheme of the organization of the ordered values |
| In the text | |