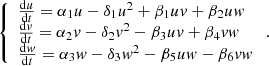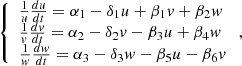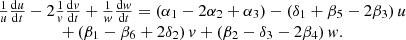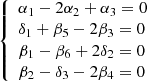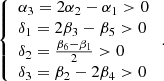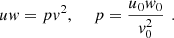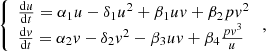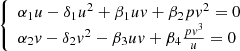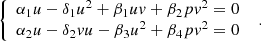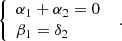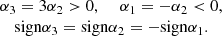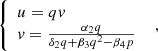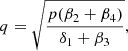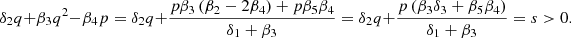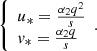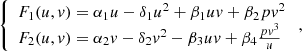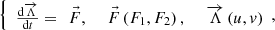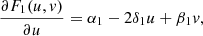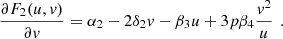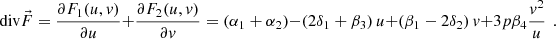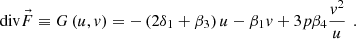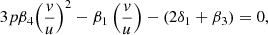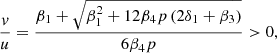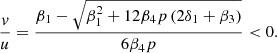| Issue |
4open
Volume 3, 2020
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 8 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2020008 | |
| Published online | 28 August 2020 | |
Research Article
Research of a three-dimensional nonlinear dynamic system describing the process of two-level assimilation
Sokhumi State University, Ana Politkovskaia st., Tbilisi, Georgia
* Corresponding author: gia.pochkhua@gmail.com
Received:
9
June
2020
Accepted:
19
July
2020
The work proposes a new general nonlinear mathematical model describing the social process of two-level assimilation taking into account quadratic members of self-restriction of population growth of three sides. In the case of constant coefficients of the model, the first integral of a three-dimensional dynamic system has been found, which in the phase space of solutions is a cone. The three-dimensional dynamic system is reduced to two-dimensional and with the help of the Bendixon’s criterion the theorem of existence in the first quarter of the phase plane of the closed integral trajectory is proved. Thus, conditions on model parameters are found that do not fully assimilate the third side.
Key words: Mathematical model / Two-level assimilation / First integral / Cone / Bendixon’s criterion
© T. Chilachava and G. Pochkhua, Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
One of the most sought-after directions of applied mathematics is mathematical modeling. To understand various complex, mostly nonlinear processes taking place in nature, in sky bodies, in the social sphere, their mathematical modeling is necessary. For more or less real description of processes it is necessary to take into account their describing basic characteristics and correctly set the corresponding mathematical problems. Mathematical modeling of physical processes involves the model adequacy, which is validated by Newton’s non-relative five laws of classical mechanics: mass conservation law; law of conservation of impulse; the law of conservation the momentum of impulse; the first law of thermodynamics, i.e. energy conservation law; the second law of thermodynamics, i.e. entropy conservation law [1–14].
Creation of mathematical models is more original in social sphere, because, they are more difficult to substantiate. We created a new direction of mathematical modeling, i.e. “Mathematical Modeling of Information Warfare” [15–17]. In these models two antagonistic sides waging with each other information warfare and also the third peacekeeping side trying to extinguish information warfare reconsidered. Conditions on model parameters at which the third side will be able to force the conflicted sides to completion of information warfare are found.
We also offered mathematical models of forecasting the results of political elections in case of two or three parties. Also models in case of change of selective subjects before the next elections have been considered [18–22].
We proposed to create new nonlinear mathematical models of economic cooperation between two politically (not military opposition) mutually warring sides (two countries or a country and its legal region) which consider economic or other type of cooperation between different parts of population aimed to the peaceful resolution of conflicts [23–29].
Taking into consideration the important tendencies in the world, it is important to study demographic and assimilation of social processes through mathematical modeling [30–32].
In [33] we considered a new nonlinear continuous mathematical model of linguistic globalization. Two categories of the world’s population are considered: a category that hinders and a category leading to the dominant position of the English language. With a positive demographic factor of the population, which prevents globalization or a negative demographic factor of the population contributing to globalization, it is shown that the dynamic systems describing these processes allow the existence of two topologically not equivalent phase portraits (a stable node, a limit cycle). It is known that, in the world, a social process of assimilation of languages is hidden. This process, as a rule, considers expansion of an area of the dominating languages (state languages of economically powerful states) at the expenses of less widespread languages (state languages economically of rather weak states). According to this point of view, today, for less widespread languages (including classic languages) the conditions under which there will be no disappearance of the major languages are important, i.e. there will be no full assimilation of people talking in these languages.
In a preceding article [34] a new nonlinear mathematical model of process of three level assimilation which is described by four-dimensional dynamic systems has been studied. In case of constancy of coefficients, special points of the dynamic system have been found. The conditions on constant coefficients for which it is possible to find special points with all four coordinates non-negative have been determined. Introducing some dependence among coefficients of the system, two first integrals have been derived, and the four-dimensional system has been reduced to a two-dimensional one. The sign-variable divergence theorem of a two-dimensional vector field in some one-coherent area of the first quadrant of the phase plane has been proved. According to Bendixon’s criterion it was shown that it is possible to have a closed integral curve completely lying in this area.
General mathematical model of two-level assimilation
System of the equations
Consider the social process of two-level assimilation, when in one large region the population speaking the most common language assimilates both the population speaking the second fairly common language and the population speaking the third less common language (small range of language distribution). In turn, the population speaking the second language, which is quite common, assimilates the population speaking the less common third language. Thus, the population speaking the third less common language is in a situation of bilateral assimilation.
We assume that the process of assimilation develops due to numerous direct or remote (electronic communication) mutual meetings between representatives of the population, who consider one of these three languages to be their native language.
The social process of two-level assimilation, which takes into account the quadratic terms of self-limiting population growth, is described by the following nonlinear dynamic system
with initial conditions:
where
-
[0, T] – the period of consideration of this model (for various cases, the period can reach several decades),
-
u(t) – at a given time t the number of people living in the same region (possibly the continent) who consider their native language in this region to be the most common language (dominant language),
-
v(t) – at a given time t the number of people living in the same region who consider their native language to be another common language in this region,
-
w(t) – at a given time t the number of people living in a small part (in a small area) of the same region who only in this part of the region consider the common language to be their native language,
-
β 1(t), β 3(t) – assimilation rates of the population speaking the second sufficiently spoken language by the population speaking the most spoken language,
-
β 2(t), β 5(t) – assimilation rates of the population speaking a third less spoken language by the population speaking the most spoken language,
-
β 4(t), β 6(t) – assimilation rates of a population speaking a third less spoken language by a population speaking a second sufficiently spoken language,
-
α 1(t), α 2(t), α 3(t) – natural change rates of populations speaking the first, second and third languages respectively (variable demographic factors),
-
δ 1(t), δ 2(t), δ 3(t) – self-limiting factors of population growth speaking the first, second and third languages respectively.
Scenario of development of two-level assimilation process is given in Figure 1.
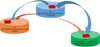 |
Figure 1 Development of two-level assimilation process. |
It is natural to assume that assimilation coefficients and growth self-constraints are positive continuous functions at the time of model consideration:
The non-triviality of the two-level assimilation process (when the assimilation result is not initially predicted) leads to inequality:
The first integral of a nonlinear system of differential equations
Second order surfaces in phase space
Consider the particular case where all model coefficients are
Taking into account (5) the system of equations (1) becomes
Find the first integral of the system of nonlinear differential equations (6) to lower the order of the system, i.e. from a three-dimensional system go to a two-dimensional one.
The dynamic system (6) shall be written in the following form
The second equation of the system (7) is multiplied by (−2) and we add all three equations (the first and third equations are unchanged)
We will require the following conditions (four conditions system) are satisfied on the model factors
or
Note that the system (10) is consistent and must meet the inequalities (3), (4).
Taking into account the imposed conditions (9) on the coefficients of the model (8), (5) we get the first integral of the dynamic system
The first integral (11) in the phase space of solutions (O, u, v, w) represents a cone.
Taking into account (11), three-dimensional dynamic system (6) can be reduced to the following two-dimensional nonlinear dynamic system
We will find non-zero (non-trivial) special points of the system (12)
Or
Let’s consider a special case
Taking into account (15), the solution of the system of nonlinear algebraic equations (14) will take the following form
where
Thus, in the first quarter of the phase plane (O, u(t), v(t)), the special point M(u *, v *) with non-zero coordinates will take the form
We put, by definition:
Then the system of equations (12) will be written in vector form
Theorem 1. The task (21) in some one-coherent area D ⊂ (O, u(t), v(t)) the first quarter of the phase plane (O, u(t), v(t)) has the decision in the form of the closed trajectory which completely lies in this area.
Proof. From (20), taking into account (21), you can get
Taking into account (22) divergence of vector field 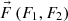 will register in the following look
will register in the following look
Taking into account (15), equation (23) takes the form
In the phase plane (O, u(t), v(t)), consider a curve where the divergence of the vector field is zero.
According to (24), this curve verifies the equation
or
whose solutions have two determinations, which identify two straight lines
Note here that second straight line does not satisfy model condition, i.e. physical meaning of u(t), v(t) functions.
Accordingly, by (26), there is only one semi-straight plane in the first quarter of the phase plane (O, u(t), v(t))
where the divergence of the vector field is zero.
At that, if equality to model parameters is performed
then the special point M(u *, v *) (19) lies on the semi-straight (27).
It is clear, that G(u,v), divergence (24) of the vector field 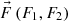 , in some one-coherent area making physical sense to the first quarter of the phase plane (O, u(t), v(t)) changes its sign (Fig. 2). Note here that single-link area comprises semi-straight section with zero divergence of vector field and, according to Bendixon criterion, there exists closed system trajectory in said area (21) [35, 36]. The theorem is proved.
, in some one-coherent area making physical sense to the first quarter of the phase plane (O, u(t), v(t)) changes its sign (Fig. 2). Note here that single-link area comprises semi-straight section with zero divergence of vector field and, according to Bendixon criterion, there exists closed system trajectory in said area (21) [35, 36]. The theorem is proved.
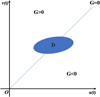 |
Figure 2 Qualitative picture of the behavior of divergence of the vector field in the first quarter of the phase plane of solutions. |
Conclusion
Thus according to (24), (27) in the phase plane (O, u, v) there exists a one-coherent area where the divergence G(u; v) of the vector field 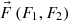 changes its sign and, according to the Bendixon criterion, in this area there exists a closed integral curve, where (u(t) ≠ 0, v(t) ≠ 0).
changes its sign and, according to the Bendixon criterion, in this area there exists a closed integral curve, where (u(t) ≠ 0, v(t) ≠ 0).
In this case, according to (11), the values of the function w(t) do not vanish anywhere, which indicates that under these conditions there is no complete assimilation of the third side.
References
- Golubiatnikov A, Chilachava T (1983), Central explosion of a rotating gravitating body. Rep Acad Sci USSR 273, 825–829. [Google Scholar]
- Golubyatnikov A, Chilachava T (1984), Estimates of the motion of detonation waves in a gravitating gas. Fluid Dyn 19, 2, 292–296. [CrossRef] [Google Scholar]
- Chilachava T (1985), Problem of a strong detonation in a uniformly compressing gravitating gas. Moscow State University, Bull Ser Math Mech 1, 78–83. [Google Scholar]
- Golubyatnikov A, Chilachava T (1986), Propagation of a detonation wave in a gravitating sphere with subsequent dispersion into a vacuum. Fluid Dyn 21, 4, 673–677. [CrossRef] [Google Scholar]
- Chilachava T (1988), A central explosion in an inhomogeneous sphere in equilibrium in its own gravitational field. Fluid Dyn 23, 3, 472–477. [CrossRef] [Google Scholar]
- Chilachava T (1996), On the asymptotic method of solution of one class of gravitation theory nonlinear problems. Reports of Enlarged Session of the Seminar of I. Vekua Institute of Applied Mathematics 11, 3, 18–26. [Google Scholar]
- Chilachava T (1997), On the solution of one nonlinear problem of mathematical physics. Reports of the Seminar of I. Vekua Institute of Applied Mathematics 23, 1–9. [Google Scholar]
- Chilachava T (1998), On the asymptotic method of solution of one class of nonlinear mixed problems of mathematical physics. Bull Georgian Acad Sci 157, 3, 373–377. [Google Scholar]
- Chilachava T (1999), On the asymptotic method of solution of one class of astrophysics problems. Appl Math Inform 4, 2, 54–66. [Google Scholar]
- Chilachava T (2007), The mathematical modeling of astrophysics problems. GESJ Comput Sci Telecommun 13, 2, 93–101. [Google Scholar]
- Chilachava T, Kereselidze N (2008), The integrodifferential inequalities method for the solving of modeling problems of Astrophysics. Sokhumi State University Proceedings, Mathematics and Computer Sciences IV, 26–56. [Google Scholar]
- Chilachava T, Tsiala D (2008), Mathematical Modeling. Tbilisi, p. 448. [Google Scholar]
- Chilachava T, Kereselidze N (2009), The integrodifferential inequalities method for the solving of modeling problems of gravitating gas dynamics. GESJ Comput Sci Telecommun 21, 4, 104–124. [Google Scholar]
- Chilachava T (2019), About the exact solutions of the rotating three-axis gas ellipsoid of Jacobi which is in own gravitational field. Reports of Enlarged Session of the Seminar of I. Vekua Institute of Applied Mathematics 33, 11–14. [Google Scholar]
- Chilachava T, Kereselidze N (2012), Optimizing problem of mathematical model of preventive information warfare, information and computer technologies “theory and practice”. Proceedings of the International Scientific Conference ICTMC- 2010 Devoted to the 80th Anniversary of I.V., Prangishvili, USA. Nova, pp. 525–529. [Google Scholar]
- Chilachava T, Kereselidze N (2011), Mathematical modeling of information warfare. Information Warfare 1, 17, 28–35. [Google Scholar]
- Chilachava T, Chakhvadze A (2014), Continuous nonlinear mathematical and computer model of information warfare with participation of authoritative interstate institutes. GESJ Comput Sci Telecommun 4 (44), 53–74. [Google Scholar]
- Chilachava T (2013), Nonlinear three-party mathematical model of elections, Problems of management of safety of difficult systems. Works XXI of the International Conference 513–516. [Google Scholar]
- Chilachava T (2013), Nonlinear mathematical model of dynamics of voters of two political subjects. Seminar of I. Vekua Institute of Applied Mathematics, Reports 39, 13–22. [Google Scholar]
- Chilachava T (2016), About some exact solutions of nonlinear system of the differential equations describing three-party elections. Appl Math Inf Mech 21, 1, 60–75. [Google Scholar]
- Chilachava T (2017), Mathematical model of transformation of two-party elections to three party elections. GESJ Comput Sci Telecommun 2, 52, 21–29. [Google Scholar]
- Chilachava T, Sulava L (2018), Mathematical and computer modeling of political elections, Of the eleventh International Scientific–Practical Conference Internet-Education Science 2018, Proceedings, pp. 113–116. [Google Scholar]
- Chilachava T, Pochkhua G (2018), Research of the dynamic system describing mathematical model of settlement of the conflicts by means of economic cooperation. GESJ Comput Sci Telecommun 3, 55, 18–26. [Google Scholar]
- Chilachava T, Pochkhua G (2018), About a possibility of resolution of conflict by means of economic cooperation. Problems of management of safety of difficult systems. The XXVI International Conference, Moscow, pp. 69–74. [Google Scholar]
- Chilachava T, Pochkhua G (2019), Research of the nonlinear dynamic system describing mathematical model of settlement of the conflicts by means of economic cooperation. 8th International Conference on Applied Analysis and Mathematical Modeling, ICAAMM 2019, Proceedings Book, pp. 183–187. [Google Scholar]
- Chilachava T, Pochkhua G, Kekelia N, Gegechkori Z (2019), Research of the dynamic systems describing mathematical models of resolution of conflict by means of economic cooperation at bilateral or unilateral counteraction. Tskhum-Abkhazian Academy of Sciences, Proceedings, Vol. XVII–XVIII, pp. 12–23. [Google Scholar]
- Chilachava T, Pochkhua G (2019), Research of the dynamic systems describing mathematical models of resolution of the conflicts by means of economic cooperation. Tskhum-Abkhazian Academy of Sciences, Proceedings, Vol. XVII–XVIII, pp. 24–37. [Google Scholar]
- Chilachava T, Pochkhua G, Kekelia N, Gegechkori Z (2019), Research of conflict resolution dynamic systems describing by mathematical models. Reports of Enlarged Session of the Seminar of I. Vekua Institute of Applied Mathematics 33, 1–4. [Google Scholar]
- Chilachava T, Pochkhua G (2019), Mathematical and computer modeling of political conflict resolution. Problems of management of safety of difficult systems. The XXVII International Conference, Moscow, pp. 293–299. [Google Scholar]
- Chilachava T, Chakaberia M (2014), Mathematical modeling of nonlinear process of assimilation taking into account demographic factor. GESJ Comput Sci Telecommun 4, 44, 35–43. [Google Scholar]
- Chilachava T, Chakaberia M (2015), Mathematical modeling of nonlinear processes bilateral assimilation. GESJ Comput Sci Telecommun 2, 46, 79–85. [Google Scholar]
- Chilachava T, Chakaberia M (2016), Mathematical modeling of nonlinear processes of two-level assimilation. GESJ Comput Sci Telecommun 3, 49, 34–48. [Google Scholar]
- Chilachava T (2019), Research of the dynamic system describing globalization process. Springer Proceedings in Mathematics & Statistics, Mathematics, Informatics and their Applications in Natural Sciences and Engineering 276, 67–78. [Google Scholar]
- Chilachava T, Pinelas S, Pochkhua G (2020), Research of four-dimensional dynamic systems describing processes of three level assimilation. Differential and Difference Equations with Applications: Springer Proceedings in Mathematics & Statistics (in print). [Google Scholar]
- Bendixson IO (1901), Sur les courbes definies par des equations differentielles. Acta Math 24, 1, 1–88. [CrossRef] [Google Scholar]
- Claudius H (1937), Rosarius Dulac Recherche des cycles limites. CR Acad. sciences 204, 23, 1703–1706. [Google Scholar]
Cite this article as: Chilachava T & Pochkhua G 2020. Research of a three-dimensional nonlinear dynamic system describing the process of two-level assimilation. 4open, 3, 10
All Figures
 |
Figure 1 Development of two-level assimilation process. |
| In the text | |
 |
Figure 2 Qualitative picture of the behavior of divergence of the vector field in the first quarter of the phase plane of solutions. |
| In the text | |


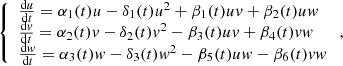
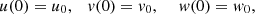
![$$ \begin{array}{c}u,\enspace {v},\enspace {w}\enspace \in {C}^1\left[0,T\right],\\ {\alpha }_i(t),{\beta }_j(t),{\delta }_i(t)\in C[0,T],\enspace {i}=\overline{\mathrm{1,3}},\enspace {j}=\overline{\mathrm{1,6}},\end{array} $$](/articles/fopen/full_html/2020/01/fopen200019/fopen200019-eq3.gif)
![$$ {\beta }_i(t)>0,\hspace{1em}\enspace {i}=\overline{\mathrm{1,6}},\hspace{1em}\enspace {t}\in \left[0,T\right], $$](/articles/fopen/full_html/2020/01/fopen200019/fopen200019-eq4.gif)
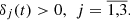
![$$ {\alpha }_3(t)>0,\enspace {t}\in \left[0,T\right]. $$](/articles/fopen/full_html/2020/01/fopen200019/fopen200019-eq6.gif)
![$$ \begin{array}{c}{\beta }_i(t)={\beta }_i=\mathrm{const}>0,\enspace {i}=\overline{\mathrm{1,6}},\enspace {t}\in [0,T],\\ {\alpha }_1(t)={\alpha }_1=\mathrm{const},\hspace{0.5em}{\alpha }_2(t)={\alpha }_2=\mathrm{const},\hspace{0.5em}{\alpha }_3(t)={\alpha }_3=\mathrm{const}>0,\\ {\delta }_1(t)={\delta }_1=\mathrm{const}>0,\hspace{0.5em}{\delta }_2(t)={\delta }_2=\mathrm{const}>0,\hspace{0.5em}{\delta }_3(t)={\delta }_3=\mathrm{const}>0.\end{array} $$](/articles/fopen/full_html/2020/01/fopen200019/fopen200019-eq7.gif)