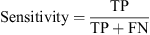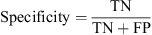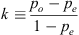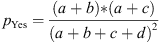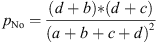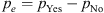| Issue |
4open
Volume 2, 2019
|
|
|---|---|---|
| Article Number | 29 | |
| Number of page(s) | 13 | |
| Section | Life Sciences - Medicine | |
| DOI | https://doi.org/10.1051/fopen/2019024 | |
| Published online | 28 October 2019 | |
Research Article
Using neural networks to predict the outcome of refractive surgery for myopia
1
Ophthalmica Institute of Ophthalmology and Microsurgery, V. Olgas 196, Thessaloniki 546 55, Greece
2
Faculty of Medicine, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece
3
Laboratory of Information Technologies, Faculty of Information Science and Informatics, Ionian University, Corfu 49100, Greece
4
Department of Ophthalmology, Cornea, Cataract and Refractive Surgery, University Eye Hospital Basel USB, Mittlere Strasse 91, 4031 Basel, Switzerland
5
Association for Training in Biomedical Technology, 6 Aristogeitonos Street, Thessaloniki 54628, Greece
* Corresponding author: anogian@hotmail.com
Received:
21
May
2019
Accepted:
24
September
2019
Introduction: Refractive Surgery (RS), has advanced immensely in the last decades, utilizing methods and techniques that fulfill stringent criteria for safety, efficacy, cost-effectiveness, and predictability of the refractive outcome. Still, a non-negligible percentage of RS require corrective retreatment. In addition, surgeons should be able to advise their patients, beforehand, as to the probability that corrective RS will be necessary. The present article addresses these issues with regard to myopia and explores the use of Neural Networks as a solution to the problem of the prediction of the RS outcome.
Methods: We used a computerized query to select patients who underwent RS with any of the available surgical techniques (PRK, LASEK, Epi-LASIK, LASIK) between January 2010 and July 2017 and we investigated 13 factors which are related to RS. The data were normalized by forcing the weights used in the forward and backward propagations to be binary; each integer was represented by a 12-bit serial code, so that following this preprocessing stage, the vector of the data values of all 13 parameters was encoded in a binary vector of 1 × (13 × 12) = 1 × 156 size. Following the preprocessing stage, eight independent Learning Vector Quantization (LVQ) networks were created in random way using the function Ivqnet of Matlab, each one of them responding to one query with (0 retreat class) or (1 correct class). The results of the eight LVQs were then averaged to permit a best estimate of the network’s performance while a voting procedure by the neural nets was used to arrive at the outcome
Results: Our algorithm was able to predict in a statistically significant way (as evidenced by Cohen’s Kappa test result of 0.7595) the need for retreatment after initial RS with good sensitivity (0.8756) and specificity (0.9286).
Conclusion: The results permit us to be optimistic about the future of using neural networks for the prediction of the outcome and, eventually, the planning of RS.
Key words: Refractive surgery / Myopia / Outcomes / Neural Networks / Ophthalmology
© M. Balidis et al., Published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
Artificial Intelligence (AI), after a tumultuous history dating back to the early 1960s, has emerged as a powerful assistant to physicians in tasks like sensing, learning, reasoning, and making decisions. Although early AI systems relied heavily on expert-derived rules for approaching these tasks, recent developments in Machine Learning (ML), especially in the sub-field of Neural Networks (NN) and deep learning, permit the development of programs that automatically “learn” to perform such tasks by processing large amounts of data.
Ophthalmology has been a beneficiary of the power of deep learning; it is, e.g., possible to use deep-learning based software to make referral recommendations that are equally valid or better than those of experts for a number of retinal diseases based on 3-dimensional Optical Coherence Tomography (OCT) [1]; to scan images for signs of diabetic retinopathy [2], alleviating thus the problem of insufficient human resources (experts) for the interpretation of the ever increasing volume and complexity of diagnostic images; to predict the progression of myopia and to detect the onset of high myopia in young adults in East and Southeast Asia, as early as 8 years in advance [3]. Finally, a statistical classifier algorithm has been developed to maximize the use of big data [4] in predicting Refractive Surgery Outcome. This particular study utilized the automated classification of multiple clinical parameters to identify a multitude of clinical factors that may contribute to unsatisfactory results and detect high-risk patients.
Refractive Surgery (RS), or the surgical correction of refractive errors of the eye, has advanced immensely in the last decades. The methods for the individualized correction of refractive errors and the techniques that are presently available fulfill stringent criteria for safety, efficacy, cost-effectiveness, and predictability of the refractive outcome [5, 6]. However, a small but not negligible percentage of RS outcomes require corrective retreatment [7–9]. Despite the small incidence of RS failures, it is extremely important that they are minimized. Basic medical ethics necessitate that the surgeon should advise his patients, before the first operation takes place, as to the probability that corrective RS will be necessary if the surgeon has the ability to determine (even approximately) such probability. In the present article, we focus on corrective RS procedures for myopia. The reason is that it is the most widely used refractive correction and, by far, the most popular among people of younger ages – with long-term effects on the patient’s quality of life. Through a selective review of the literature and of the authors’ personal experience stemming from more than 4500 RS procedures to correct myopia, as well as a thorough search of the Ophthalmica Institute of Ophthalmology and Microsurgery, Thessaloniki, Greece (thereafter designated as “Ophthalmica”), we present our effort to resolve the issue of predicting the probability of success of corrective retreatment procedures for myopia through data mining, neural networks and deep learning technologies.
Pre-method explanation
The refractive apparatus of the eye
The refractive apparatus of the eye consists of the cornea, the anterior chamber, the lens, and the vitreous humor. They are functionally grouped into the corneal system and the lens system. The refractive power of the corneal system is about 40–50 diopters, while that of the lens system is much less, about 15–25 diopters. Astigmatism arises when either or both the cornea and the lens have a different curvature, and therefore a different refractive power, in two meridians. When this is the case, the uneven refraction of a light ray that is incident upon the eye results in the projection of a displaced or distorted image onto the retina, rather than a point image. Finally, another refractive error is presbyopia that is due to the gradual loss of flexibility of the lens that occurs during the fifth decade of life, rendering it unable to accommodate, i.e., to increase its refractive power for near vision.
Refractive surgical techniques in Refractive Corneal Surgery (RCS)
There are two established surgical methods for the correction of refractive error: Refractive Corneal Surgery (RCS) and Refractive Lens Surgery (RLS). RCS uses Excimer (“excited dimer”) laser techniques with or without Femtosecond laser technology and incisional procedures; RLS involves Phakic Intraocular Lenses (PIOL) and Refractive Lens Exchange (RLE). The present report is focused on RCS with Excimer laser techniques for the correction of myopia.
Excimer laser techniques use an argon fluoride laser operating at the wavelength of 193 nm. There are two types of excimer laser RCS procedures: Surface treatment techniques and Lamellar treatment techniques. In RCS, the cornea is remodeled with laser ablation. The aim of the surgical intervention is to direct the light rays falling upon the eye to focus precisely on the macula (where vision is sharpest).
In the surface treatment techniques, the corneal tissue is ablated just below the corneal epithelium. The techniques include Photorefractive Keratectomy (PRK), Laser-Subepithelial Keratomileusis (LASEK), and Epi-LASIK. Before ablation, the corneal epithelium is removed using laser (in PRK), alcohol solution (in LASEK), or is mechanically separated (using a microkeratome) from the underlying tissue (in epi-LASIK). Following ablation, the corneal epithelium is restored back in place.
The lamellar treatment technique combines a separation of anterior stroma, creating a circular hinged flap and excimer laser ablation, known as Laser in Situ Keratomileusis (LASIK). A microkeratome or a femtosecond laser is used to cut a flap which is folded back to have access to the stromal tissue of the cornea and, in contrast to the surface treatment techniques, in LASIK laser ablation is performed in the anterior stroma. Following ablation, the flap is put back into its original position, where it is held by adhesive forces and the endothelial Na/K ATPase pump activity. There, it becomes permanently fixed in place by tissue growth within a few hours. The femtosecond laser carries a lower risk of a cutting error than the mechanical microkeratome and it avoids the occurrence of Delayed Hypersensitivity Syndrome (DHS). In addition, the time needed for visual rehabilitation is roughly the same whether the corneal flap is created with femtosecond laser or with a microkeratome.
To correct myopia, the excimer laser is used to ablate and reshape the anterior surface of the cornea and reduce the refraction. To adjust the ablation profile more precisely, “eye trackers” registering the position of the iris are used to correct for horizontal, vertical, and rotatory eye movements. An eye tracker is a pursuit system that ensures the removal of corneal tissue at the intended location and prevents accidental decentering of the ablation zone. It can compensate for ocular saccades that occur during treatment. If the patient should suddenly make a large-amplitude eye movement, the ablation procedure is interrupted.
Indications and contraindications for RCS in myopia
According to the guidelines of the German Commission for Refractive Surgery [10] LASEK, PRK, LASIK, epi-LASIK can be used for the correction of myopia up to –8 dpt (with LASIK for myopia up to –10 dpt). The use of these techniques is contraindicated in the presence of symptomatic cataract, glaucoma with marked visual field damage, or exudative macular degeneration. In addition, preoperative corneal thickness <500 microns, is a further contraindication for the lamellar surgical procedures and, in such cases, superficial procedures are recommended for the correction of refractive errors.
How often does RCS for myopia require retreatment?
When compared to LASIK, the potential adverse effects of PRK, LASEK, epi-LASEK treatments include superficial corneal scarring (haze), more persistent refractive fluctuations and longer visual rehabilitation [11]. However, with increasing experience and the introduction of newer techniques, they have become very rare and their frequency is estimated at 0.5% [12]. A transiently dry eye is a common complication after LASIK. It is caused by the transection of corneal nerves by the flap incision. This, results in reduced secretion of the tear film. The eye becomes as moist as it was before surgery within 6 months after the procedure. Finally, in very rare cases, keratectasia [13] and infection [14] may occur.
In contrast, however, to potential adverse effects of RCS, failure to achieve the desired outcomes and subsequent need for retreatment is only partially dependent on patient characteristics, like age and degree of myopia. It also, among other causes, depends on the technology used, the surgical skill, and the prevailing environmental conditions during the operation. More important, all these factors apparently determine the outcome interacting with each other in ways that, at present, have not been described in the literature. A thorough search of the relevant literature gives a wide variation (1.00%–27.50%) for the percentage of RCS treatments for myopia that require retreatment, with a good estimate for the average to be of the order of 2.5%–3.00%. Table 1 is a representative – but by no means exhaustive – list of 12 studies from around the world of RCS that required retreatment that was conducted during the last decade [15–26].
Representative list of studies from around the world, conducted during the last decade, of RCS that required retreatment.
Patients and methods
The design of the present study followed the tenets of the Declaration of Helsinki. The study protocol was approved by the institutional review board committee of Ophthalmica. Data were obtained through the computerized database registry of Ophthalmica. The Database Registry includes patient demographic and clinical data variables, archived by an advanced computerized electronic record-keeping software system (Professional Clinic by Terasoft©). Records at Ophthalmica are updated by the center’s staff prospectively, during each patient’s visit. For the present study, we used a computerized query to select patients who underwent RS with any of the available surgical techniques (PRK, LASEK, Epi-LASIK, LASIK) by any of the 15 Ophthalmica surgeons whose cases contributed to the present study over the period from January 2010 to July 2017. We investigated 13 factors which are related to RS. These are:
-
Age of the subject.
-
Temperature in the operation room.
-
Humidity in the operation room.
-
Axis of astigmatism in the operated eye in degrees (0° correspond to the right corner and 180° to the left corner of the eye).
-
The thickness of the corneal stroma.
-
Type of surgical technique: (i.e., PRK, LASEK, Epi-LASIK, LASIK)
-
Laser ablation method (i.e., Asphericity value-based ablation, Standard wavefront optimized ablation or Topographic guided ablation)
-
The keratometric value for the horizontal axis of the cornea.
-
The keratometric value for the vertical axis of the cornea.
-
The maximum laser intensity applied during the intervention on the cornea.
-
The minimum laser intensity applied during the intervention on the cornea.
-
The maximum laser voltage applied during the intervention on the cornea.
-
The minimum laser voltage applied during the intervention on the cornea.
Data preprocessing stage
The normalization of the above 13 parameters affects the choice of the right training procedure for the neural network so that it can arrive at a decision. The problem arises because the data values of the input parameters are real numbers with non-significant decimal part, and there is wide variability among the ranges for the individual parameters. It should be noted that the training procedure for neural networks is very sensitive to this kind of data. Indeed, neural networks can easily counteract the application of normalization by scaling the weights and changing the bias – a problem that becomes evident, in the training procedure for the resilient back propagation algorithm. Although, in theory, it is not necessary to normalize numeric data (also called independent data) when the numeric data values are normalized; the neural network training often becomes more efficient, and a better predictor [27].
Most of the computations performed during the training and application of deep networks regard the multiplication of the real-valued weights by the real-valued activation (during the recognition or forward propagation phase of the back-propagation algorithm) or by the gradient (during the backward propagation phase of the back-propagation algorithm) [28]. In the present paper, we propose an approach to normalization which eliminates these multiplications by forcing the weights used in the forward and backward propagations to be binary [28]. In our case, each integer is represented by a 12-bit serial code. The 12-bit encoding is adopted in view of the size and the negativity of the integers used. In this way, following this preprocessing stage, the vector of the data values of all 13 parameters is encoded in a binary vector of 1 × (13 × 12) = 1 × 156 size.
Data classification stage
A Learning Vector Quantizer (LVQ) neural network is employed for classification in the present work. LVQ was preferred to other candidate types of networks, such as Multi-Layer Perceptron (MLP), because of its non-linear classification properties [27]. Learning Vector Quantization (LVQ) neural networks comprise two layers. The first layer maps input vectors into clusters that are determined by the network during learning. The second layer consolidates them, beginning with layer clusters, into classes characterized by the target data.
The architecture of LVQ in the learning procedure
The first step in the design of LQV neural network is to set the parameters of both competitive and linear layers. The available input data vectors are divided into training and test groups. The learning algorithm, generally, performs as follows:
Codebook initialization
A number of the codebook vectors for each target group are compared with the number of occurrences for that group and these vectors are initialized to the center of the input ranges. In our case, we created two training groups (the retreat group and the non-retreat group). The training of LVQ is a two-step procedure. In the first step, initial positions of the class representatives (or codebook vectors) are determined in the r-dimensional space using standard clustering algorithms such as the K-Means or the Linde–Buzo–Gray algorithm (LBG) algorithm, with a given number of classes. In the second step, class representative positions are iteratively updated so that the total classification error of the training set of vectors is minimized. To this end, codebook vectors are directed towards the data vectors of the same class and distanced from the data vectors of different classes [29, 30].
The winner decision
The Euclidean distance is calculated between the training data vector and the codebook vector. Specifically, every time a member of the training set, feature vector pi, is incorrectly classified, the two codebook vectors involved [correct r c (i−1) and incorrect r w (i−1)] are updated as follows:
The LVQ network is designed by the weights of the competition layer through self-organization, using a number of the training input vectors, to reflect the distribution of the sample data patterns in the output layer. LVQ pattern recognition algorithm is derived from the Kohonen competitive algorithm [25, 27]. The architecture of the LVQ network is depicted in Figure 1. According to this architecture, an input vector p with R dimensionality is used. Furthermore, the competitive number of the neurons in the layer is denoted as S 1. The connection of the weight coefficient matrix between input and competition is depicted as IW1.1. The input to the competition layer neuron is symbolized with n 1; the a 1 symbol expresses the competition layer neuron and the LW2.1 stands for the connection weight coefficient matrix which is extracted by the competition between the comparative layers and the linear output layer [31]. Furthermore, the symbols n 2 expresses the input of the linear output layer; the a 2 is the linear output layer neuron.
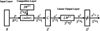 |
Figure 1 Architecture of the LVQ neural network. |
 |
Figure 2 Individual performance of Ophthalmica surgeons regarding their retreatments/treatment ratios, r = −0.06352. |
The output of the training procedure (output vector y) for either the correct or non-retreat case is calculated as follows:
The simulated net is calculated as:
During the testing procedure, the constructed net (Eq. (2)) is simulated using the sim function and reacts with an unknown vector p 1 as follows:
The decision resulting from the testing procedure is extracted according to the error difference (e) between the output y vector (see Eq. (2)) and the reconstructed vector y net (see Eq. (4)) yields two values (0 or 1) according to equation (5)
Voting stage by neural nets
Information aggregation in neural nets is a procedure of joint decision-making. In the proposed system, a new query vector is tested against each of the K two-way classifiers in order to be determined if it belongs to the given class or not. This class (correct) determines with a significant probability the success corneal laser RS while the other class (retreat) correspondingly determines the unsuccessful surgery outcome. This leads to K scores from the K classifiers. The idea is to obtain an unambiguous prediction for a given testing vector [32, 33]. This is achieved by reducing or eliminating false positives. In our study, all votes from the eight classifiers are tallied and the class with the most votes represents the final prediction. The number eight was chosen to achieve an eight-bit form of voting. Therefore, the false positive problem is eliminated at this second step of the decision stage. Note that in the false positives elimination step, the decision boundary is drawn between two “true” classes of training vectors, instead of between one “true” class and its complementary “others” class, which is highly complex. Thus, false positives are eliminated accurately. Thus, the proposed decision system (considering Eq. (4)) is constructed as follows:
and
then the neural nets voting system (considering Eq. (5)) gives the following classification’s decision:
It must be noted that, in the retreat case we adopted a larger scale than the case of the correct class in order to increase the specificity. This took place because we set stricter criteria should be used for securing the decision on the case of the correct class.
Experimental part
Between the 1st of July 2010 and the 13th of July 2017, a total of 4456 RS operations were performed by 15 ophthalmic surgeons in Ophthalmica. Of these 4372 were original treatments and 84 corrective retreatments. Overall retreatment/treatment ratio was 0.01885, well within the lower range of the international experience (Tab. 1). The experience of the individual surgeons correlated only slightly but definitely in a statistically not significant manner (p = 0.823496!) with outcome (r for number of treatments vs % of retreatments = −0.06352).
Of these operations 2378 non-retreat and 70 retreat cases were isolated based on follow-up that confirmed successful completion of the procedure for over a year. The rest were not used in our experiment, either because of incomplete data on record (regarding each and every one of the 13 parameters examined; see “Patients and methods” above) or because they did not return for a follow-up after 1 year so that the long-term success of RS or retreatment could be confirmed.
Data preprocessing stage
In this experiment, 2308 vectors of the non-retreat or correct and 70 vectors of retreat cases are used. These vectors are constructed according to the description in the preprocessing stage. The normalization procedure is implemented via the section “Data preprocessing stage”. In the binary implementation each element of a feature vector p f (the original with 13 features) was coded using the same number of bits.
To enable a quick run time decoding, each element occupied its own position of bits per element. The precision of such an approach depends (for a fixed domain size) on the number of n = 12 bits actually used, and equals (DB − LB)/(2n − 1), where DB and LB are domain bounds and n is the number of bits per one element of a feature. Thus, a binary vector p size (1 × 156) is constructed.
Thus, we create matrix R with the retreat (12 bit) binary vectors and matrix C with the correct or non-retreat binary vectors as follows:
Neural network training stage
Following the preprocessing stage, eight independent LVQ networks were created in random way. Each one of the LVQ networks responds to one query with (0 retreat class) or (1 correct class). Each neural network has the following characteristics according to section Refractive surgical techniques in refractive corneal surgery:
-
S (number of neurons = 78).
-
The number of epochs i = 100 (see Eq. (1)).
-
The number of each training vectors for both groups is 30, which are chosen in a random way from the total number of 2308 vectors. Then two groups (c-correct, r-retreat case) 388 of vectors are constructed. Each vector consists of 156 parameters.
-
The above stage is repeated eight times in a random procedure so that eight neural LVQ networks are constructed. Each time, the procedure continues (Tab. 3) until the mean square error is minimized within ≤100 numbers of epochs.
Table 3Results for a neural network constructed of 78 neurons, following training for ≤100 epochs (see Eq. (1)). The number of each training vector for both treatment and retreatment groups is 30. Each time, the procedure continues until the mean square error is minimized within the ≤100 number of epochs. Following the training procedure, two groups (c-correct case and r-retreat case) of vectors are constructed (see Eq. (9)). The procedure is repeated eight times with randomly constructed training vectors so that eight equivalent but different neural LVQ networks are constructed. The results of the eight repetitions are then averaged to permit a best estimate of the network’s performance.
-
The results of the eight repetitions are then averaged to permit a best estimate of the network’s performance.
Voting stage by neural nets
Considering equations (6)–(8), we constructed two groups of testing vectors. The first group concerns the non-retreat or correct case with 2308 vectors and the retreat case with 70 vectors. Thus, we have two voting procedures using the eight independent LVQ networks from Neural Network Training Stage, while the equations (6)–(8) are transformed as follows:
and
then the equation (5) is transformed accordingly and comes to the following classification’s decision:
Results
The neural classification test is a valid single test which could predict the possible outcome of the RS, i.e., to predict whether the operative outcome will meet presurgical planning and expectations or the cornea will require retreatment. It is necessary therefore to have the statistical means to decide whether the neural network employed in our case indeed makes meaningful predictions. In other words, it is necessary to determine the validity of the prediction. Validity is measured by means of the sensitivity and specificity of the test which, for our case, are best illustrated by a conventional two- by-two (2 × 2) table (Tab. 4) which compares the outcome of RS in terms of cases that required no retreatment (non-retreat case) versus those that required retreatment (retreat case).
Terms of the sensitivity and specificity measurements.
Measuring sensitivity, specificity, and Cohen’s Kappa statistic (k-Cohen).
In Table 4, cell a contains the cases where the neural classification test correctly diagnosed a retreat case as such; these are the True Positives (TP). Cell b contains the cases where the neural classification test misdiagnosed a non-retreat case as a retreat case; these are the False Positives (FP). Cell c contains the cases where the neural classification test misdiagnosed a retreat case as a non-retreat case; these are the False Negatives (FN). Finally, cell d contains the cases where the neural classification test correctly diagnosed a non-retreat case as such; these are True Negatives (TN).
Based on the above description, sensitivity and specificity are calculated as follows:
When assessing of whether a test (e.g., a radiograph) is helpful to clinicians, it is important for its interpretation to be precise, i.e., not the product of guesswork. A useful analogy is that of hitting a target and how close one gets to the bull’s-eye [34]. When one actually hits the bull’s-eye (i.e., agrees with the gold standard), they are precise. When all their shots land together, they display good reliability. When all their shots land together, and they hit the bull’s-eye, they are precise and reliable.
In our case, the important question we had to answer is (a) how different are the results of the neural classification test (“observed” agreement) from the difference that is expected by chance alone (“expected” agreement) and (b) what the statistical significance of our findings in this respect is. Cohen’s Kappa is a measure of this difference, and it varies between −1 and 1, where 1 is perfect agreement, 0 is exactly what would be expected purely by chance, and negative values indicate agreement less than chance, i.e., some degree of systematic disagreement between the results of the neural classification test and the actual data (which serve as the gold standard). Then the visualization of the interpretation of kappa test (see Tab. 7) gives the scale of the agreement between −1 and 1 value [34].
Voting procedure: measuring sensitivity, specificity, and Cohen’s Kappa statistic (k-Cohen)
The definition of Cohen’s Kappa is given by equation (18) and considering the parameters of Table 2:
where p o (see Eq. (19)) is the relative observed agreement among raters (who are identical as to their accuracy), and p e (see Eq. (22)) is the hypothetical probability of chance agreement, using the observed data to calculate the probabilities of each observer randomly seeing each category. If the raters are in complete agreement, then k = 1. If there is no agreement among the raters other than what would be expected by chance (as given by p e ), k = 0. It is possible for the statistic to be negative [35], which implies that there is no effective agreement between the two raters or the agreement is worse than random.
In cell a, we enter those in whom the test in question correctly diagnosed the retreat case and these are the True Positives (TP).
In cell b, we enter those who have positive results for the test in question but do not have retreat case. The newer test has wrongly predicted the retreat case: These are False Positives (FP).
In cell c, we enter those who have retreat cases but have negative results with the test in question. The test has wrongly labeled a non-retreat case as “retreat”. These are False Negatives (FN).
In cell d, we enter those who have non-retreat case and are also negative. These are True Negatives (TN).
According to above equations the calculation of the sensitivity and specificity and Cohen’s Kappa statistic are calculated using the data of Table 3 and are depicted in Table 5.
As can be seen in Tables 5 and 6, the values of the Cohen’s Kappa test, the sensitivity and the specificity are ranged (0.6552–0.7369), (0.6571–0.7466) and (0.6924–0.7385) correspondingly. Also, the results of the voting procedure (Tab. 7) improved the values both in the indexes of the sensitivity (0.8756), specificity (0.9286) and the testing Cohen’s Kappa test (0.7595) significantly. Furthermore, according to Table 8 (Cohen’s Kappa test) these results indicate substantial agreement of the classification results with actual outcome.
Interpretation of Kappa.
Discussion
Despite the immense advances in RS over the last few decades and the stringent criteria for safety, efficacy, cost-effectiveness, and predictability of the refractive outcome [5, 6] that have been introduced, a small but not negligible percentage of RS outcomes require corrective retreatment [7–9]. Although the incidence of RS failures in certain clinics has declined (2-year annual retreatment rates) from 4.52% for primary surgeries done in 2005 to 0.18% for surgeries performed in 2012 [18] and, generally, is extremely low there is still room for improvement. Furthermore, exactly because of the low rates of retreatments that have been achieved, it is important for surgeons to be able to advise their patients, before the first operation takes place, as to the probability that corrective RS may be necessary. In the opposite case, they leave themselves open to questions about the procedure they have followed in the case of an inferior to golden standard outcome that could, otherwise, have been predicted.
Conclusion
In the present article, we focused on predicting the potentially unsatisfactory outcome of corrective RS procedures for myopia. The reason is that myopia represents the most widely used refractive correction and is, by far, the most popular reason that people of younger ages resort to a corrective procedures which also have significant and beneficial long-term effects on the patient’s quality of life. To achieve our stated goal, we utilized the Ophthalmica clinical records to set up a neural network-based algorithm that predicts the probability of success/failure of corrective retreatment procedures for myopia.
Recently published research on the issue of the predicting RS outcome [4] was based on case studies of patients who underwent LASIK or photorefractive surgeries over a period of 12 years. In that case, the relevant dataset was converted to binary vectors that were then submitted to training and testing procedures using machine-learning classifiers. Prediction efficacy was based on 38 clinical parameters (binary vector) which were classified into subspaces so that each subspace constituted the basis for a different prediction. In contrast, our present study investigates the possible relation of the numerical representation of 13 clinical parameters in a consolidated way by using an artificial neural network. In this way the complexity of this procedure is decreased significantly, and the system output represents a clinical decision by identifying the high-risk patients who are candidates for RS.
Of the 13 parameters utilized by our neural network-based algorithm, five are measurable patient characteristics (age of the subject, axis of astigmatism in the eye to be operated (in degrees), thickness of the corneal stroma, keratometric value for the horizontal axis of the cornea and keratometric value for the vertical axis of the cornea), while the other eight can be decided by the operating surgeon who can thus utilize our neural network-based algorithm not only to predict the outcome of RS but also to potentially optimize the parameters (temperature and humidity in the operation room, surgical technique – i.e., PRK, LASEK, Epi-LASIK, LASIK and laser ablation method – i.e., asphericity value-based ablation, standard wavefront optimized ablation or topographic guided ablation – along with maximum and minimum laser intensities, as well as maximum and minimum laser voltages applied during the intervention on the cornea) he/she plans to use in his/her surgical approach to RS for the specific patient. When interpreting kappa cohen index, it is also important to keep in mind that the estimated kappa index in this study is 0.7595 (see Tab. 7). Then, considering Table 8, this value gives a substantial agreement in the hypothesis that the two groups (c-correct, r-retreat) are separated with a statistic significance [34].
The statistically significant improvement (as evidenced by Cohen’s Kappa test result of 0.7595) of both the sensitivity (0.8756) and specificity (0.9286) of the results of our neural network-based algorithm, makes us optimistic about the future. This study suggests that selecting a better activation function can significantly improve the performance of an LVQneural network.
Nomenclature of Abbreviations
DHS: Delayed Hypersensitivity Syndrome
Epi-LASIK: Epipolis Laser In situ Keratomileusis
LASEK: Laser-Subepithelial Keratomileusis
LASIK: Laser In Situ Keratomileusis
LBG algorithm: Linde–Buzo–Gray algorithm
LVQ: Learning Vector Quantization
PIOL: Phakic Intraocular Lenses
PRK: Photo Refractive Keratectomy
RCS: Refractive Corneal Surgery
Conflict of interest
Each and every one of the authors unequivocally state that they have no conflict of interest, regarding all facts, equipment, and procedures involved in this work.
References
- De Fauw J, Ledsam JR, Romera-Paredes B, Nikolov S, Tomasev N, Blackwell S, Askham H, Glorot X, O’Donoghue B, Visentin D, van den Driessche G, Lakshminarayanan B, Meyer C, Mackinder F, Bouton S, Ayoub K, Chopra R, King D, Karthikesalingam A, Hughes CO, Raine R, Hughes J, Sim DA, Egan C, Tufail A, Montgomery H, Hassabis D, Rees G, Back T, Khaw PT, Suleyman M, Cornebise J, Keane PA, Ronneberger O (2018), Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat Med 24, 9, 1342–1350. https://doi.org/10.1038/s41591-018-0107-6. [CrossRef] [PubMed] [Google Scholar]
- Lee KJ (2018), AI device for detecting diabetic retinopathy earns swift FDA approval, American Academy of Ophthalmology, CA, USA. Available from https://www.aao.org/headline/first-ai-screen-diabetic-retinopathy-approved-by-f. Accessed January 7, 2019. [Google Scholar]
- Lin H, Long E, Ding X, Diao H, Chen Z, Liu R, Huang J, Cai J, Xu S, Zhang X, Wang D, Chen K, Yu T, Wu D, Zhao X, Liu Z, Wu X, Jiang Y, Yang X, Cui D, Liu W, Zheng Y, Luo L, Wang H, Chan CC (2018), Prediction of myopia development among Chinese school-aged children using refraction data from electronic medical records: A retrospective, multicentre machine learning study. PLoS Med 15, 11, 1–17. https://doi.org/10.1371/journal.pmed.1002674. [Google Scholar]
- Achiron A, Gur Z, Aviv U, Hilely A, Mimouni M, Karmona L, Rokach L, Kaiserman I (2017), Predicting refractive surgery outcome: Machine learning approach with big data. J Refract Surg 33, 9, 592–597. https://doi.org/10.3928/1081597X-20170616-03. [CrossRef] [PubMed] [Google Scholar]
- Kohnen T (1999), Kriterien zur Evaluierung und Publikation von refraktiv-chirurgischen Eingriffen (Editorial). Klin Monatsbl Augenheilkd 215, 6, 326–328. PMID: 10637793. [CrossRef] [Google Scholar]
- Koch DD, Kohnen T, Obstbaum SA, Rosen ES (1998), Format for reporting refractive surgical data. J Cataract Refract Surg 24, 3, 285–287. PMID: 9559453. [PubMed] [Google Scholar]
- Pokroy R, Mimouni M, Sela T, Munzer G, Kaiserman I (2016), Myopic laser in situ keratomileusis retreatment: Incidence and associations. J Cataract Refract Surg 42, 10, 1408–1414. https://doi.org/10.1016/j.jcrs.2016.07.032. [PubMed] [Google Scholar]
- Yuen LH, Chan WK, Koh J, Mehta JS, Tan DT, SingLasik Research Group (2010), A 10-year prospective audit of LASIK outcomes for myopia in 37,932 eyes at a single institution in Asia. Ophthalmology 117, 6, 1236–1244. https://doi.org/10.1016/j.ophtha.2009.10.042. [Google Scholar]
- Randleman JB, White AJ Jr, Lynn MJ, Hu MH, Stulting RD (2009), Incidence, outcomes, and risk factors for retreatment after wavefront-optimized ablations with PRK and LASIK. J Refract Surg 25, 3, 273–276. PMID: 19370822. [CrossRef] [PubMed] [Google Scholar]
- Kohnen T, Neuhann T, Knorz MC (2011), Bewertung und Qualitätssicherung refraktiv-chirurgischer Eingriffe durch die DOG und den BVA, Stand Mai 2011. Ophthalmologe 108, 869–882. https://doi.org/10.1007/s00347-011-2415-9. [CrossRef] [PubMed] [Google Scholar]
- Kohnen T (2000), Retreating residual refractive errors after excimer surgery of the cornea: PRK versus LASIK. J Cataract Refract Surg 26, 5, 625–626. PMID: 10831879. [PubMed] [Google Scholar]
- Kohnen T, Strenger A, Klaproth OK (2008), Basic knowledge of refractive surgery: Correction of refractive errors using modern surgical procedures. Dtsch Arztebl Int 105, 9, 163–172. https://doi.org/10.3238/arztebl.2008.0163. [PubMed] [Google Scholar]
- Pallikaris IG, Kymionis GD, Astyrakakis NI (2001), Corneal ectasia induced by laser in situ keratomileusis. J Cataract Refract Surg 27, 11, 1796–1802. PMID: 11709254. [PubMed] [Google Scholar]
- Moshirfar M, Welling JD, Feiz V, Holz H, Clinch TE (2007), Infectious and noninfectious keratitis after laser in situ keratomileusis Occurrence, management, and visual outcomes. J Cataract Refract Surg 33, 3, 474–483. https://doi.org/10.1016/j.jcrs.2006.11.005. [PubMed] [Google Scholar]
- Hersh PS, Fry KL, Bishop DS (2003), Incidence and associations of retreatment after LASIK. Ophthalmology 110, 4, 748–754. https://doi.org/10.1016/S0161-6420(02)01981-4. [Google Scholar]
- Siedlecki J, Luft N, Kook D, Wertheimer C, Mayer WJ, Bechmann M, Wiltfang R, Priglinger SG, Sekundo W, Dirisamer M (2017), Enhancement after myopic small incision lenticule extraction (SMILE) using surface ablation. J Refract Surg 33, 8, 513–518. https://doi.org/10.3928/1081597X-20170602-01. [CrossRef] [PubMed] [Google Scholar]
- Kruh JN, Garrett KA, Huntington B, Robinson S, Melki SA (2017), Risk factors for retreatment following myopic LASIK with femtosecond laser and custom ablation for the treatment of myopia. Semin Ophthalmol 32, 3, 316–320. https://doi.org/10.3109/08820538.2015.1088552. [PubMed] [Google Scholar]
- Mimouni M, Vainer I, Shapira Y, Levartovsky S, Sela T, Munzer G, Kaiserman I (2016), Factors predicting the need for retreatment after laser refractive surgery. Cornea 35, 5, 607–612. https://doi.org/10.1097/ICO.0000000000000795. [CrossRef] [PubMed] [Google Scholar]
- Valdez-García JE, Hernandez-Camarena JC, Martínez-Muñoz R (2016), 3-year follow-up after Lasik: Assessing the risk factors for retreatment. Int Ophthalmol 36, 1, 91–96. https://doi.org/10.1007/s10792-015-0084-4. [CrossRef] [PubMed] [Google Scholar]
- See B, Tan M, Chia SE, Gan WH, Low R, Nah G (2014), Photorefractive keratectomy in young Asian aviators with low-moderate myopia. Aviat Space Environ Med 85, 1, 25–29. PMID: 24479255. [CrossRef] [PubMed] [Google Scholar]
- Gazieva L, Beer MH, Nielsen K, Hjortdal J (2011), A retrospective comparison of efficacy and safety of 680 consecutive lasik treatments for high myopia performed with two generations of flying-spot excimer lasers. Acta Ophthalmol 89, 8, 729–733. https://doi.org/10.1111/j.1755-3768.2009.01830.x. [CrossRef] [PubMed] [Google Scholar]
- Yuen LH, Chan WK, Koh J, Mehta JS, Tan DT (2010), A 10-year prospective audit of LASIK outcomes for myopia in 37,932 eyes at a single institution in Asia. Ophthalmology 117, 6, 1236–1244.e1. https://doi.org/10.1016/j.ophtha.2009.10.042. [Google Scholar]
- Shojaei A, Mohammad-Rabei H, Eslani M, Elahi B, Noorizadeh F (2009), Long-term evaluation of complications and results of photorefractive keratectomy in myopia: An 8-year follow-up. Cornea 28, 3, 304–310. https://doi.org/10.1097/ICO.0b013e3181896767. [CrossRef] [PubMed] [Google Scholar]
- Bragheeth MA, Fares U, Dua HS (2008), Re-treatment after laser in situ keratomileusis for correction of myopia and myopic astigmatism. Br J Ophthalmol 92, 11, 1506–1510. https://doi.org/10.1136/bjo.2008.143636. [CrossRef] [PubMed] [Google Scholar]
- Alió JL, Muftuoglu O, Ortiz D, Pérez-Santonja JJ, Artola A, Ayala MJ, Garcia MJ, de Luna GC (2008), Ten-year follow-up of laser in situ keratomileusis for high myopia. Am J Ophthalmol 145, 1, 55–64. https://doi.org/10.1016/j.ajo.2007.08.035. [CrossRef] [PubMed] [Google Scholar]
- Alio JL, Galal A, Artola A, Ayala MJ, Merayo J (2006), Hyperopic LASIK retreatments with the Technolas laser. J Refract Surg 22, 6, 596–603. PMID: 16805124. [CrossRef] [PubMed] [Google Scholar]
- McCaffrey JD (2013), Neural network training using particle swarm optimization, Dec 18, 2013, Visual Studio Magazine. https://visualstudiomagazine.com/Articles/2013/12/01/Neural-Network-Training-Using-Particle-Swarm-Optimization.aspx?Page=1&p=1. Accessed January 7, 2019. [Google Scholar]
- Courbariaux M, Bengio Y, David JP (2015), Binaryconnect: Training deep neural networks with binary weights during propagations, Advances in Neural Information Processing Systems, 28, 3124–3131. https://papers.nips.cc/paper/5647-binaryconnect-training-deep-neural-networks-with-binary-weights-during-propagations.pdf. [Google Scholar]
- Langari R, Won JS (2005), Intelligent energy management agent for a parallel hybrid vehicle-part I: System architecture and design of the driving situation identification process. IEEE Trans Veh Technol 54, 3, 925–934. https://trid.trb.org/view/762206. [Google Scholar]
- Poulos M, Rangoussi M, Alexandris N, Evangelou A (2002), Person identification from the EEG using nonlinear signal classification. Methods Inf Med 41, 1, 64–75. PMID: 11933767. [CrossRef] [PubMed] [Google Scholar]
- Papavlasopoulos S, Poulos M, Evangelou A (2006), Feature extraction from interictal epileptic and non-epileptic pathological EEG events for diagnostic purposes using LVQ1 neural network, in: Mathematical Methods in Scattering Theory and Biomedical Engineering, World Scientific, pp. 390–398. https://doi.org/10.1142/9789812773197_0038. [CrossRef] [Google Scholar]
- Ding CH, Dubchak I (2001), Multi-class protein fold recognition using support vector machines and neural networks. Bioinformatics 17, 4, 349–358. PMID: 11301304. [CrossRef] [PubMed] [Google Scholar]
- Kim BK, Roh J, Dong SY, Lee SY (2016), Hierarchical committee of deep convolutional neural networks for robust facial expression recognition. J Multimodal User Interfaces 10, 2, 173–189. https://doi.org/10.1007/s12193-015-0209-0. [CrossRef] [Google Scholar]
- Viera AJ, Garrett JM (2005), Understanding interobserver agreement: The kappa statistic. Fam Med 37, 5, 360–363. PMID: 15883903. [PubMed] [Google Scholar]
- Sim J, Wright CC (2005), The kappa statistic in reliability studies: Use, interpretation, and sample size requirements. Phys Ther 85, 3, 257–268. PMID: 15733050. [PubMed] [Google Scholar]
Cite this article as: Balidis M, Papadopoulou I, Malandris D, Zachariadis Z, Sakellaris D, et al. 2019. Using neural networks to predict the outcome of refractive surgery for myopia. 4open, 2, 29.
All Tables
Representative list of studies from around the world, conducted during the last decade, of RCS that required retreatment.
Results for a neural network constructed of 78 neurons, following training for ≤100 epochs (see Eq. (1)). The number of each training vector for both treatment and retreatment groups is 30. Each time, the procedure continues until the mean square error is minimized within the ≤100 number of epochs. Following the training procedure, two groups (c-correct case and r-retreat case) of vectors are constructed (see Eq. (9)). The procedure is repeated eight times with randomly constructed training vectors so that eight equivalent but different neural LVQ networks are constructed. The results of the eight repetitions are then averaged to permit a best estimate of the network’s performance.
Voting procedure: measuring sensitivity, specificity, and Cohen’s Kappa statistic (k-Cohen)
All Figures
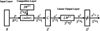 |
Figure 1 Architecture of the LVQ neural network. |
| In the text | |
 |
Figure 2 Individual performance of Ophthalmica surgeons regarding their retreatments/treatment ratios, r = −0.06352. |
| In the text | |


![$$ \begin{array}{l}{{\mathbf{r}}_c}^{(i)}\mathrm{\enspace }=\mathrm{\enspace }{{\mathbf{r}}_c}^{(i-1)}\mathrm{\enspace }+\mathrm{\enspace }a(i)\left[{p}_i\mathrm{\enspace }-\mathrm{\enspace }{{\mathbf{r}}_c}^{(i-1)}\right],\\ {{\mathbf{r}}_w}^{(i)}\mathrm{\enspace }=\mathrm{\enspace }{{\mathbf{r}}_w}^{(i-1)}\mathrm{\enspace }-\mathrm{\enspace }a(i)\left[{p}_i\mathrm{\enspace }-\mathrm{\enspace }{{\mathbf{r}}_w}^{(i-1)}\right].\enspace \end{array} $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq1.gif)
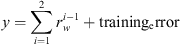
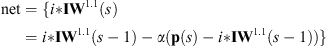
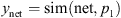
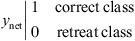
![$$ S=\left[\begin{array}{c}\sum_{i=1}^n{y}_{\mathrm{ne}{\mathrm{t}}_1}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_1,{p}_i)\\ \sum_{i=1}^n{y}_{\mathrm{ne}{\mathrm{t}}_2}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_2,{p}_i)\\ \begin{array}{c}\vdots \\ \sum_{i=1}^n{y}_{\mathrm{ne}{\mathrm{t}}_8}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_8,{p}_i)\end{array}\end{array}\right] $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq6.gif)
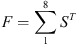
![$$ \mathrm{if}\hspace{1em}\begin{array}{cc}F>4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{correct}& \forall \enspace F\enspace \in \enspace \left[5,\dots,8\right]\\ F\le 4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{retreat}& \forall \enspace F\enspace \in \enspace \left[0,\dots,4\right]\end{array} $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq8.gif)
![$$ {\vec{p}}_f=\left[\begin{array}{l}{\vec{f}}_1\\.\\.\\.\\ {\vec{f}}_{13}\end{array}\right]\enspace \mathrm{where}\hspace{1em}{f}_1=\left[\begin{array}{l}{a}_1\\.\\.\\.\\ {a}_{12}\end{array}\right],{f}_2=\left[\begin{array}{l}{a}_{13}\\.\\.\\.\\ {a}_{124}\end{array}\right],\dots {f}_{13}=\left[\begin{array}{l}{a}_{144}\\.\\.\\.\\ {a}_{156}\end{array}\right]\enspace \mathrm{where}\hspace{1em}{a}_{j=1,\dots,156}\in \enspace \left[\mathrm{0,1}\right] $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq9.gif)
![$$ \vec{p}=\left[\begin{array}{l}{a}_1\\.\\.\\.\\ {a}_{j=156}\end{array}\right] $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq10.gif)
![$$ \begin{array}{cc}R=\left[\begin{array}{l}{\vec{p}}_{r1}\\.\\.\\.\\ {\vec{p}}_{r70}\end{array}\right]& \mathrm{and}\hspace{1em}C=\left[\begin{array}{l}{\vec{p}}_{c1}\\.\\.\\.\\ {\vec{p}}_{c2308}\end{array}\right]\end{array}\enspace $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq11.gif)
![$$ \begin{array}{cc}r=\left[\begin{array}{l}{\vec{p}}_{r1}\\.\\.\\.\\ {\vec{p}}_{r30}\end{array}\right]& \enspace \mathrm{and}\hspace{0.5em}c=\left[\begin{array}{l}{\vec{p}}_{c1}\\.\\.\\.\\ {\vec{p}}_{c30}\end{array}\right]\end{array} $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq12.gif)
![$$ {S}_1=\left[\begin{array}{l}\sum_{i=1}^{2308}{y}_{\mathrm{ne}{\mathrm{t}}_1}=s\mathrm{im}(\mathrm{ne}{\mathrm{t}}_1,{p}_i)\\ \sum_{i=1}^{2308}{y}_{\mathrm{ne}{\mathrm{t}}_2}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_2,{p}_i)\\.\\.\\.\\ \sum_{i=1}^{2308}{y}_{\mathrm{ne}{\mathrm{t}}_8}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_8,{p}_i)\end{array}\right]\enspace \wedge \enspace {S}_2=\left[\begin{array}{l}\sum_{i=1}^{70}{y}_{\mathrm{ne}{\mathrm{t}}_1}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_1,{p}_i)\\ \sum_{i=1}^{70}{y}_{\mathrm{ne}{\mathrm{t}}_2}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_2,{p}_i)\\.\\.\\.\\ \sum_{i=1}^{70}{y}_{\mathrm{ne}{\mathrm{t}}_8}=\mathrm{sim}(\mathrm{ne}{\mathrm{t}}_8,{p}_i)\end{array}\right] $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq13.gif)
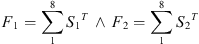
![$$ \begin{array}{c}\mathrm{if}\hspace{1em}\begin{array}{cc}{F}_1>4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{correct}& \forall \enspace {F}_1\enspace \in \enspace \left[5,\dots,8\right]\\ {F}_1\le 4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{retreat}& \forall \enspace {F}_1\enspace \in \enspace \left[0,\dots,4\right]\enspace \end{array}\\ \wedge \hspace{1em}\begin{array}{cc}{F}_2>4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{correct}& \forall \enspace {F}_2\enspace \in \enspace \left[5,\dots,8\right]\end{array}\\ \mathrm{if}\hspace{1em}\begin{array}{cc}{F}_2\le 4\enspace \to \enspace \in \enspace \mathrm{class}\enspace \mathrm{retreat}& \forall \enspace {F}_2\enspace \in \enspace \left[0,\dots,4\right]\end{array}\end{array} $$](/articles/fopen/full_html/2019/01/fopen190018/fopen190018-eq15.gif)