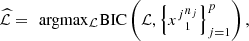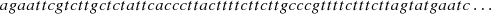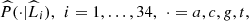| Issue |
4open
Volume 2, 2019
Statistical Inference in Copula Models and Markov Processes, Case Studies and Insights
|
|
|---|---|---|
| Article Number | 25 | |
| Number of page(s) | 7 | |
| Section | Mathematics - Applied Mathematics | |
| DOI | https://doi.org/10.1051/fopen/2019020 | |
| Published online | 11 July 2019 | |
Research Article
Stochastic profile of Epstein-Barr virus in nasopharyngeal carcinoma settings
1
Department of Mathematics, Federal University of Technology, Avenida Monteiro Lobato, s/n – Km 04, Ponta Grossa, CEP 84016-210 Paraná, Brazil
2
Department of Statistics, University of Campinas, Sergio Buarque de Holanda, 651, Campinas, CEP 13083-859 São Paulo, Brazil
* Corresponding author: jg@ime.unicamp.br
Received:
3
March
2019
Accepted:
6
June
2019
We build a profile of the Epstein-Barr virus (EBV) by means of genomic sequences obtained from patients with nasopharyngeal carcinoma (NPC). We consider a set of sequences coming from the NCBI free source and we assume that this set is a collection of independent samples of stochastic processes related by an equivalence relation. Given a collection {(Xjt)t∈ℤ}pj=1 of p independent discrete time Markov processes with finite alphabet A and state space S, we state that the elements (i, s) and (j, r) in {1, 2,…, p} × S are equivalent if and only if they share the same transition probability for all the elements in the alphabet. The equivalence allows to reduce the number of parameters to be estimated in the model avoiding to delete states of S to achieve that reduction. Through the equivalence relationship, we build the global profile for all the EBV in NPC sequences, this model allows us to represent the underlying and common stochastic law of the set of sequences. The equivalence classes define an optimal partition of {1, 2,…, p} × S, and it is in relation to this partition that we define the profile of the set of genomic sequences.
Key words: Partition Markov Models / Bayesian Information Criterion / Transition probability
© M.T.A. Cordeiro et al., Published by EDP Sciences, 2019
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
The purpose of this paper is to produce an economical model which allows representing the genomic organization of the Epstein-Barr virus (EBV), considering DNA sequences of EBV, obtained from patients with nasopharyngeal carcinoma (NPC), a disease with a distinctly high incidence in southern China. To investigate the role of EBV genomic in the pathogenesis of NPC it is necessary to describe the EBV in NPC settings. It is suggested that EBV may play a role in the development of NPC, as no other type of tumor in humans is as consistently associated with EBV as NPC. Despite the fact that EBV infection is ubiquitous, the incidence of NPC presents a remarkable geographic pattern, as it is approximately 100 times more frequent in North Africa, Southeast Asia, and Alaska than in the rest of the world. In this paper, we use two complete sequences known in the literature: GD1 [1] and GD2 [2] and an incomplete sequence, HKNPC1, reported in [3]. Phylogenetic analysis of strains in [3] also includes other sequences of EBV but not in NPC settings, and it shows that HKNPC1 is more closely related to the Chinese NPC patient-derived strains, GD1 and GD2. This evidence supports our idea to build a unique model using these three sequences.
When referring to an economical model, we are thinking about the notion introduced in [4], given in Section 2. In this article, we treat the sequences as samples of Markovian processes. By idealizing an economical model we can appeal to the principle of minimality. In the context of Markovian processes, a certain notion of minimality can be applied to the state space. Some of the ways to treat the problem are: (i) reducing the state space itself, (ii) reducing the number of probabilities to be estimated. For instance, (i) by applying deterministic finite automaton theory, to minimize an auxiliary Markov chain state space (see [5]). For (ii) by applying partition Markov models (see [6]). In the present work, we will use the second perspective, since it does not delete any state, which is relevant in our case for the characterization of EBV in NPC.
The preliminaries and the notions that we use as well as the definition of the model are given in Section 2. The model estimation is given in Section 3. We detail the database, and we show the results in Section 4, and the final considerations in Section 5.
Preliminaries
Denote by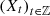 
a discrete time Markov chain, with a finite alphabet and finite order. Consider 
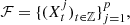a collection of p independent, discrete time, Markov chains on the same finite alphabet A. To simplify the notation we will assume that all the processes have the same finite memory o. S = A
o
is the state space of each Markov chain in the collection. Then, each string in S is a concatenation of o elements of the alphabet A. Denote the string a
m
, a
m+1,…, a
n
by 
where a
i
∈ A, m ≤ i ≤ n. Given the process j of the collection 
and a time t, the event 
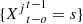means that the process is equal to s in the o positions, immediately prior to the position on time t, 
For each j ∈ J = {1, 2,…, p}, a ∈ A and s ∈ S,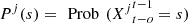 
and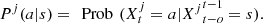 
We define now the space where the model is established M = J × S.
The parameters to be estimated in this situation are the conditional probabilities, and without the assumption of identical distribution, there are |A|−1 probabilities, for each state s and each process j. This corresponds to a total of p(|A|−1)|A| o parameters. Consider the situation in which there are two processes, i and j and two states s, r ∈ S such that P i (a|s) = P j (a|r) for all a ∈ A, then just one group of probabilities is necessary to estimate, this produces a reduction in the total number of parameters to be estimated. With this situation in mind, the following model is considered.
Definition 2.1.
The elements (i, s), (j, r) ∈ M, are equivalent if P i (a|s) = P j (a|r) for all a ∈ A.
This concept is very flexible in the sense that i and j could also be the same. Thus, the idea is to group all the pairs (i, s) and (j, r) that share the same probabilities and define with them, parts that constitute a partition of M.
Definition 2.2.
A collection of p indepedent processes
has a Markov partition
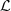= {L
1, L
2,..., L
k
} if
is the partition of M defined by the relationship introduced in
Definition 2.1
. Each element L
i
of
is a part of the partition.
Note that under the Definition 2.2, each element (i, s) ∈ L, where L is a part of 
is such that i ∈ {1,…, p} and s ∈ 
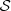. And note that 
of the Definition 2.2 is minimal in the sense of having the smallest possible k, since it represents the relation of equivalence given in the Definition 2.1. Furthermore, once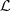 
is identified, we can also identify the conditional probabilities of the 
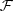collection, effectively reducing the number of parameters of the model. Given 
, we will have the following collection of parameters,
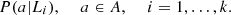(1)Then, the total number of parameters to estimate is 
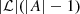. The process of estimating 
requires a strategy, because as we will see, the identification of the minimal partition can be a fairly exhaustive process.
In the example given below we expose the notion introduced in the Definition 2.1.
Example 2.1.
Consider three processes with alphabet A = {0, 1} and conditional probabilities P
i
(⋅|s), i = 1, 2, 3 given by
Table 1
(left) with
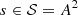. We report the parts which compound the partition
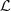of
in the
Table 1
(right).
Left: conditional probabilities for the processes 1, 2 and 3. Right: parts of partition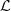 
of M.
The number of probabilities considering the three processes separately is 12 ( Table 1 – left), while by the identification made by the Definition 2.1 the number of probabilities becomes 5 ( Table 1 – right).
Model estimation
Let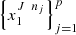 
be samples of the processes 
with sample sizes 
Then, 
can constitute a collection of independent and identically distributed realizations of one single stochastic process or only be a collection of independent realizations, coming from different processes. This means that the usual assumption (in statistical estimation) of the existence of an underlying and single law is replaced by the notion introduced in [1] and also reproduced by Definitions 2.1 and 2.2, so, the law established by Definition 2.2 is the law of the set. The number of occurrences of s ∈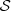 
in the sample 
is denoted by N((j,s)) and the number of occurrences of s followed by a in the sample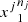 
is denoted by N((j, s), a). Given a partition 
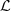as refered in Definition 2.2, the number of occurrences of elements in L is N(L) = ∑(i,s)∈L
N((i,s)), L ∈ 
and the number of occurrences of elements in L followed by a ∈ A is, N(L, a) = ∑(i,s)∈L
N((i, s), a). The estimator based on the Bayesian Information Criterion (BIC), associated to the samples and for the partition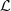 
of M is,
(2)Based on results derived from [6], when min{n
1,…, n
p
} → ∞, eventually almost surely,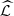 
= 
of Definition 2.2.
Definition 3.1.
Let
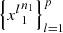be samples of the collection
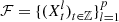of p independent Markov chains of discrete time on the same finite alphabet A with finite order o. For (i, s), (j, r) ∈ M = {1,…, p} × A
o
, set,
where N({(i, s), (j, r)}) = N((i, s)) + N((j, r)) and N({(i, s), (j, r)}, a) = N((i, s), a) + N((j, r), a).
This is a metric on M, related to the BIC criterion in the following way, the BIC criterion indicates that (i, s), (j, r) ∈ M should be in the same part if and only if d((i, s), (j, r)) < 1. d is also statistically consistent to decide if (i, s), (j, r) ∈ M or not (see [6]). The metric given in Definition 3.1 goes to zero, when the laws P i (⋅|s) and P j (⋅|r) are identical and it takes very large values when those laws are different and when the sample sizes (n i and n j ) grow.
Given the order o, we can define the state space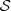 
and also the space M, and then, we can compute all the values of d in order to determine the estimator 
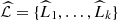of the partition 
(Definition 2.2). From the conception given by the Definition 2.1, the elements of a part share their probabilities, so we can also estimate the conditional probabilities P(⋅|L), by means of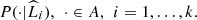 
Then, we can determine all the parameters involved in the model, proposed by the Definition 2.1.
To find the parts, the use of d can be linked to different clustering criteria: average, single linkage, agglomerative, etc. The criterion used in this work is the agglomerative, described here. Suppose that the space M is given by M = {m 1,…, m |M|}, define,
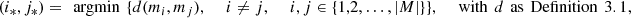(3)if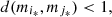 
define 
with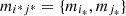 
and go back to equation (3), otherwise the procedure ends. That is, by detecting the labels i* and j* that indicate the globally closest elements in M, if they verify d < 1 then, they can be inserted in the same part, becoming an element of the new space M which is the element 
The process is repeated until there are no elements such that d is less than 1.
Data and results
EBV genomes
The datasets were obtained from http://www.ncbi.nlm.nih.gov/ (National Center for Biotechnology Information [NCBI]). GD1 was isolated by infecting umbilical cord mononuclear cells by EBV from saliva of a NPC patient. GD2 and HKNPC1 were direct isolates from primary NPC biopsy specimens, see Table 2.
EBV genomes isolated from NPC patients.
The coding of the sequences is exemplified below, showing the beginning of the GD1 sequence,
The alphabet A has cardinal |A| = 4 and it is composed by the four bases: adenine (a), cytosine (c), guanine (g) and thymine (t), A = {a, c, g, t}. The set J is given by {1, 2, 3}, with 1 referring to sequence GD1, 2 referring to sequence GD2 and 3 referring to sequence HKNPC1. In stochastic processes the memory o allowed is such that o < log|A| (n)−1, where n is the sample size, coming from the data. In this case n = 508 236 which is around the sum of the sample sizes of the three sequences, then o < 8. In the modeling problem of genomic sequences the elements of A are given in triples, so o = 3, 6 are the recommended orders. Our main results are coming from the estimation with order o = 3, since those are more easier to expose for the reader.
Estimation
In Tables 3 and 4 we show the results with order o = 3. In Table 3 we see the estimate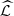 
of the partition 
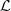which is composed by 34 estimated parts. For each estimated part 
we also inform its composition, listings from left to right and from top to bottom according to the order (magnitude of d) as they have been included in that part. In the last column we recorded the highest value of d, denoted by d*, which was found by the construction of the part, applying the agglomerative criterion (see last paragraph of Section 3). In Table 4 we show the conditional probabilities of each estimated part, see equation (1).
From top to bottom, the list of the 34 estimated parts 
(of 
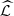), its elements to the right and in the last column the value d*. 1 referring to GD1, 2 referring to GD2 and 3 referring to HKNPC1, A = {a, c, g, t}, o = 3, 
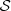= A
o
. In bold letter the largest and the lowest values of d*, and on the left, the parts which have the highest probabilities (>0.4) to one element of the alphabet A (see Table 4).
To illustrate the estimation process of each part, we will take as an example the part 31 constituted by three elements (1, cga), (2, cga), (3, cga). In a first stage the elements (1, cga), (2, cga) were joined, with a d = 0.00512 (see Definition 3.1), this is,
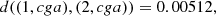later, this group of two elements was joined to the element (3, cga), with a d = 0.00815, see the right column in Table 3. Since (1, cga) and (2, cga) are considered identical, we can joint all the ocurrences of cga in the sequences GD1 and GD2. Then, for each element v of the alphabet, v ∈ A, N((1, cga), v) + N((2, cga), v) records the ocurrences of cga followed by v and N((1, cga)) + N((2, cga)) records the ocurrences of cga in the group {(1, cga), (2, cga)}. In the second stage, the metric between the group {(1, cga), (2, cga)} and (3, cga) is also computed using d from Definition 3.1,
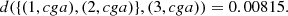Since both values of d are lower than 1, the three processes show the same stochastic law in relation to state cga but processes GD1 and GD2 are even more similar in relation to that state.
We see from the last column of Table 3, that some parts show greater homogeneity between their elements, is the case of part 34. And other parts, almost reach the limit allowed d = 1, exposing greater diversity, for example, part 1. This exposes the relevance of having a threshold that allows us to decide, in the light of some consistent criterion, when a discrepancy is actually detected (see [4, 6]).
In relation to the magnitud of the conditional probabilities, we see from Table 4 that there is a tendency in all the parts to choose as the next element to visit c or g, except in the case of part 9. We also see that there are few parts that have conditional probabilities > 0.4, we identify those parts in bold letter in Table 3 (left column). For example, looking at part 31, we see a greater tendency to form the composition cgag (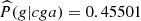
). Now seeing the last three elements gag (members of part 3) we see that although the probability of forming gagg is high, it has fallen in relation to the previous composition (
).
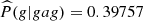In Table 5 we compare general aspects of three adjustments, varying the order: (i) o = 3, (ii) o = 4 and (iii) o = 6. We record the performance of the models for each order (each line of the Table 5).
We see that as expected the value of the BIC (and the value of maximum log-likelihood [MLL]) increases as the order of the model increases, indicating a better performance. But at the same time the number of parts quadruple from order 3 to order 6, which is why we preferred to present this study with order 3. In any case we can find the results in the following link: http://www.ime.unicamp.br/~jg/spebv/.
Conclusion
Using the model proposed in [4] we find a global representation for the three genomic sequences of Epstein-Barr virus in NPC. As we see in Example 2.1, the model foresees a reduction in the total number of parameters to be estimated and, for its estimation, we use the notion 3.1, which allows us to use different samples and different states to estimate a single probability. Taking into account the evidences of other works in relation to the similarity that these sequences show (see [3]), we take advantage of the three sequences to estimate with higher quality the parameters of the model (we use several sequences and several states for that). Also we offer a representation of the dynamic of the common process, by means of the estimated partition of the state space. We identify 34 minimum units (parts) that represent the generating process of the three sequences, and those define the partition (model). We identify the states of each part that can be considered stochastic synonyms because they produce identical transition probabilities. Note that some parts are more homogeneous than others in relation to the distance between their elements (see Table 3) and, for this reason, it is very useful to have available a threshold to use together with the metric d, this threshold is d = 1. In relation to the magnitude of the transition probailities of each part for the elements {a, c, g, t}, we note that those are in general < 0.4, and only six parts exceed this value in transitions for c or for g (see Table 4). With this specific case of a collection of genomic sequences of EBV in NPC, we show that although differences can be recognized between the sequences, an unique stochastic profile can be defined to the collection of sequences, when the members of the collection keep common aspects, such as being EBV in NPC.
Acknowledgments
M. Cordeiro and S. Londoño gratefully acknowledge the financial support provided by CAPES with fellowships from the PhD Program in Statistics – University of Campinas. J.E. García and V.A. González-López gratefully acknowledge the support provided by the project Inhibitory deficit as a marker of neuroplasticity in rehabilitation grant 2017/12943-8, São Paulo Research Foundation (FAPESP). Also, the authors wish to thank the three referees for their many helpful comments and suggestions on an earlier draft of this paper.
References
- Zeng MS, Li DJ, Liu QL, Song LB, Li MZ, Zhang RH, Yu XJ, Wang HM, Emberg I, Zeng YX (2005), Genomic sequence analysis of Epstein-Barr Virus strain GD1 from a nasopharyngeal carcinoma patient. J Virol 79, 24, 15323–15330. [CrossRef] [PubMed] [Google Scholar]
- Liu P, Fang X, Feng Z, Guo YM, Peng RJ, Liu T, Huang Z, Feng Y, Sun X, Xiong Z, Guo X, Pang SS, Wang B, Lv X, Feng FT, Li DJ, Chen LZ, Feng QS, Huang WL, Zeng MS, Bei JX, Zhang Y, Zeng YX (2011), Direct sequencing and characterization of a clinical isolate of Epstein-Barr virus from nasopharyngeal carcinoma tissue by using next-generation sequencing technology. J Virol 85, 21, 11291–11299. [CrossRef] [PubMed] [Google Scholar]
- Kwok H, Tong AH, Lin CH, Lok S, Farrel PJ, Kwong DL, Chiang AK (2012), Genomic sequencing and comparative analysis of Epstein-Barr Virus genome isolated from primary nasopharyngeal carcinoma biopsy. PLoS One 7, 5, e36939. [CrossRef] [PubMed] [Google Scholar]
- García Jesús E, Londoño SLM (2018), Optimal model for a set of Markov processes, AIP Conference Proceedings of ICNAAM 2018, vol. 2116. [Google Scholar]
- Martin DEK, Aston JAD (2013), Distributions of statistics of hidden state sequences through the sum-product algorithm. Methodol Comput Appl Probab 15, 4, 897–918. [Google Scholar]
- García JE, González-López VA (2017), Consistent estimation of partition Markov models. Entropy 19, 4, 160. [CrossRef] [Google Scholar]
Cite this article as: Cordeiro MTA, García JE, González-López VA & Londoño SLM 2019. Stochastic profile of Epstein-Barr virus in nasopharyngeal carcinoma settings. 4open, 2, 25.
All Tables
Left: conditional probabilities for the processes 1, 2 and 3. Right: parts of partition of M.
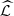From top to bottom, the list of the 34 estimated parts (of ), its elements to the right and in the last column the value d*. 1 referring to GD1, 2 referring to GD2 and 3 referring to HKNPC1, A = {a, c, g, t}, o = 3, 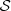= A
o
. In bold letter the largest and the lowest values of d*, and on the left, the parts which have the highest probabilities (>0.4) to one element of the alphabet A (see Table 4).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.