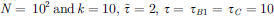Search
Menu
All issues Volume 6 (2023) 4open, 6 (2023) 3 Full HTML
Open Access
Issue
4open
Volume 6, 2023
Article Number 3
Number of page(s) 8
Section Life Sciences - Medicine
DOI https://doi.org/10.1051/fopen/2023002
Published online 07 March 2023

© D. Korošak et al., Published by EDP Sciences, 2023

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Introduction

The concept that living cells compute is almost trivial, yet the very nature of biological computation itself is much harder to precisely define, model and describe [1]. This is even more difficult when we search for these answers in analogies between computations performed by a cell collective and by Turing machine or man-made digital computational architecture [2]. Biological systems operate in an information rich, fluctuating and noisy environment from which they must extract clues in an attempt to successfully respond and adapt to a change. Physiological processes that underlie such biological information processing [3] and decision making often involve a phase transition where a sudden change of the state of the system is observed when a control parameter crosses some critical value. It was therefore posited that it would be beneficial if biological systems were to reside near a critical point [4] of a phase transition such that it could provide optimal conditions for biological computations [5].

Here we consider homeostatic regulation of nutrients and other metabolic intermediates in higher animals as one of many biological computational problems that organisms are continuously solving to ensure their survival and reproduction. The main task of this computation is to supply the metabolic code in the form of hormones like insulin or glucagon to economize with metabolites. The metabolites can be either invested into cell housekeeping to support integrity of the cell structure and function, they can be stored into cellular depots for the future use, or they are maintained in the circulating blood as a metabolic liquidity to pay for current or acutely emerging energetic requirements. This metabolic liquidity is maintained even during long periods of complete starvation [6]. On the other hand, a deleterious hormonal perturbation that leads to an exaggerated transport of glucose into the cells easily pushes an organism into hypoglycemia with glucose levels below 3.9 mmol/l. The resulting metabolic liquidity issues limit the function of immune cells, neurons and red blood cells, which by number represent a vast majority (90%) of all cells in the human body, and lead to a major acute stress response with long-term consequences [7]. The metabolic economy is therefore a key physiological process, driven by small pancreatic endocrine cell collectives, mostly insulin-secreting beta-cells, which are, packed into collectives of a few hundred cells (also called islets), distributed all over the pancreas. They sense, communicate, compute and respond with a precise hormone release to metabolic changes using a combination of intra- and intercellular, as well as inter-islet, communication mechanisms.

It is an open question how the abovementioned cell and islet collectives could act as agents and have an agenda [8], a job that has traditionally been reserved for vast neuronal networks in central nervous system. There is no particular reason why insulin-releasing cells would not acquire agency. First, on the molecular level, the spectrum of proteins expressed by pancreatic beta-cells overlaps significantly with proteins expressed in neurons. Second, although a single islet harbors only an overseable number of a few hundred beta-cells organized as a sparse cell collective of an islet [9], the total number of beta-cells distributed in the pancreas can be compared to the number of photoreceptors in the retina, which is widely appreciated as a sophisticated sensory system. It is quite possible that this agenda is encoded by intricate communication between the units as well as between the levels of distributed organization of beta-cells, involving several biological levels of explanation [10].

What do we know about the function of beta-cell collectives so far? There are two specific features of beta-cell collective response to nutrient stimuli that have been well documented in the past: dependence of beta-cell activation, expressed as cytosolic Ca2+ or membrane potential oscillations on extracellular glucose concentration, and the biphasic nature of cytosolic Ca2+ dynamics and insulin release.

The biphasic kinetics of insulin release following a supra-physiological rapid-onset and sustained glucose stimulation has been first described more than half a century ago in human [11], rat [12] and mouse pancreas [13]. Ever since its discovery, several mechanisms have been proposed to describe this biphasity, ranging from cytosolic [Ca2+]c handling from both intracellular [14] and extracellular Ca2+ sources [15], insulin granule release probability [16–18], inositol phosphate production [19], and potentiating and inhibiting metabolic influences [20].

The dual, Ca2+ and metabolic, oscillatory model had been previously used in an attempt to describe slow oscillations with a period between 5 and 10 min observed in isolated islets [19]. In more in situ preparation, like fresh pancreas tissue slices, a physiological stimulatory glucose concentration reproducibly triggers much faster and shorter [Ca2+]c oscillations with time scales too fast to support the involvement of the metabolic oscillators, however the biphasity is still evident [21]. Furthermore, tissue slice preparation helped us to uncover new evidence regarding the function of intracellular Ca2+ receptors underlying fast changes of the [Ca2+]c in addition to previously described sources [22, 23]. Based on these novel data, the concept congruent with all previously described mechanisms, including two independent mechanisms with sequent activation of inositol-1,4,5-trisphosphate (IP3) and ryanodine intracellular Ca2+ receptors, and incorporating several time scales of Ca2+-induced-Ca2+ release (CICR) has been demonstrated [22–24]. These two mechanisms support a robust asynchronous initial activation, as well as a long-term activity stimulated with a repetitive or prolonged exposure to glucose.

In this paper we model the empirically observed activation of beta-cell collectives with coupled stochastic oscillators and discuss how the combination of the abovementioned two [Ca2+]c oscillatory modes fulfills all the criteria for an effective biological computation in determining the metabolic code. We suggest that particular spatial organization of the beta-cell agents on at least two levels of biological organization and the blood perfusion pattern render pancreas as an ultimate analytical and computational instrument for a successful long-term metabolic economy. We show that to capture the whole spectrum of responses of this type of biological computation needs to employ dual mode switching, sensing precision adjustment, response adaptivity and memory.

Model and results

Collective activity model

The typical response of the beta-cell collective activity at different glucose concentrations is shown in Figure 1A. Here, we present beta-cell Ca2+ activation as a function of a parameter p defined as the time from the high glucose onset scaled with the half-time of activation (i.e., time interval in which half of cells activate) at the particular stimulus concentration. The response curves show two distinct behaviors with respect to glucose concentration: fast and abrupt transition to activity at high concentrations (16 mM and 12 mM), and more gradual transition into the active state at lower glucose concentration (7 mM; Fig. 1A).

thumbnail Figure 1

Empirical data showing glucose-dependent beta-cell activation and coupled stochastic oscillators model results. Glucose-dependent activity (A), from left to right: 16 mM, 12 mM, and 7 mM, data from [21], size of giant component of correlation networks (B). Parameters used in model calculations: random regular network with N = 102 and k = 10, T = 105, . Noise Σ = 0, 0.1, 3, 7. Threshold value for correlation networks was set to c0 = 0.1.

The presence of at least two distinct mechanisms with stochastic properties and the versatility of Ca2+ release toolkit [14, 25–27] allow us to start building models to better explain the activation of the beta-cell collectives. We map the succession of Ca2+ events onto the coupled stochastic oscillators model [28] represented with a network where each node can be in one of three states σi = {σA, σB, σC}, and with the dynamics depending on the current state of the network f ∈ [0, 1] given by the fraction of nodes in the active state σC. Each node repeats the cycle: . Dynamics in state σA is stochastic in the sense that period τA, the time interval a node spends in σA, is randomly chosen from exponential distribution: . State σB is deterministic, but nodes in state σB choose their waiting time depending on the state of the network and the threshold parameter p: they wait in state σB with period τB1 if f < p, or with τB2 if f > p. Here τB1 > τB2, so by switching to longer waiting times, the nodes that sense larger than threshold network state (f > p) tend to keep the network activity close to p. Nodes are active in the state σC for time period τC in which they output a signal to all other nodes.

Analysis and simulations of the original model [28] showed that the phase of such an all-to-all network depends on the value of the threshold parameter p. For very small values of p almost all nodes stay in one mode and the collective network dynamics is stochastic with completely unsynchronized nodes activity. As p approaches critical value pc, the nodes start to switch between the two modes resulting in network transition into synchronised phase with oscillatory collective dynamics with period τ + τB2 + τC.

In our model here, we place N cells on a random regular network where each node has k nearest neighbors. The ith cell senses the states of cells in Mi, the set of cells with the size mi = |Mi| that provide input to the ith cell. We include the sensing precision of the cell that depends on the glucose concentration as the variance of mi at each time step. At high glucose concentrations (corresponding to 16 mM in Fig. 1A) each cell has exactly k nearest neighbors. At lower concentrations the number of neighbors fluctuates with Σ, a model parameter, that increases with diminishing glucose concentration. The rationale here is that as we approach the sensory threshold, beta-cells must increase their sensory precision which requires extending the communication with other cells in the islet. We model this neighborhood fluctuation by sampling additional number of neighbors from normal distribution for each cell at each timestep. The cell compares its total input ) to the value of the threshold parameter p and chooses the appropriate σB state. The transition to coherent collective state at p = pc is possible only for . We focus on the region of p values where the network changes from stochastic to oscillatory collective dynamics.

Following our previous approach where we transcripted the dynamics into correlation networks and studied their properties [29, 30], we let the model run for T timesteps at particular value of the control parameter p to obtain N timeseries xi of nodes activity. From these N timeseries we constructed correlation networks of cells and followed the dependence of the size of the largest component C on control parameter p. Starting with an empty network, for each pair of nodes i, j we computed their cross-correlation cij = 〈xi, xj〉 and compared it to the chosen threshold value c0. If cij > c0 a link between i and j was placed in the network. Leaving the threshold c0 fixed, the density of network increased with increasing p along with activity coherence, and at particular critical value pc a phase transition in the size of largest cluster from C⁄N ≈ 0 to C⁄N ≈ 1 was observed (Fig. 1B). Figure 1B shows the results of the model computations of largest component C(p,Σ)N as a function of model parameters p and Σ. At low values of Σ the response was abrupt, showing first-order like phase transition. With increasing Σ, the cells were able to explore their wider network neighborhood, sense more distant signals effectively increasing their interaction length and thus sensing precision [31]. This mode corresponds to the case of lower glucose concentrations where cells need to precisely determine the stimulus level and the response curve now resembles second-order like phase transition.

Response adaptivity and memory

The variability of responses of beta-cells to stimulatory glucose has been demonstrated before [21, 23, 32]. This issue has, however, not being systematically addressed for repetitive stimulations of the same islet. Figure 2 shows an analysis of a recording of all beta-cells in an islet that were captured in one optical plane, as they were repeatedly stimulated with short pulses of supraphysiological glucose concentration (Fig. 2B). Beta-cells were distinguished by the significantly higher level of activity in comparison to other cells in the neighborhood (Fig. 2A). As described above, 16 mM glucose was a strong stimulus that after a short delay caused a fast and abrupt transition to activity. The analysis of the temporal profile of the duration of events showed that initial short events (subsecond and second long events) progressively started to merge into longer events lasting for some tens to hundreds of seconds, until the glucose overload slowly washed out into a resting state. Two phenomena could be observed during repetitive stimuli. First, the progressively reduced number of initially elicited short events due to swifter temporal summation, which could be a sign of the memory effect due to previous exposures. Second, the pattern of activity of long events during the prolonged activity phase differed between different stimuli, with either a pattern of exchanging ranges of long events (pulse 1 and 3) or a dominance of mostly shorter-range long events (pulse 2 and 4). It is possible that we would be able to record the whole spectrum of different responses if it would be feasible to repeat such a pulsatile stimulation for a prolonged period of time. This second feature indicated that the response of the cells showed a certain degree of adaptivity to the stimulation. It is important to mention that both features have been previously reported to be present in the physiological range of glucose, however this has not been discussed further [33].

thumbnail Figure 2

Response adaptivity and memory. (A) Regions of interest (ROIs) obtained by our segmentation algorithm [23]. The color indicates the number of events identified in the ROI trace, upon a high-pass filtering at 0.2 Hz. We discarded ROIs with number of events below the threshold (red dashed line in the histogram in the lower panel). Indicated are the ROI numbers whose filtered traces correlate best with the average trace for the whole islet. The most active cells indicated with blue tones present beta-cell in the core of the islet. (B) Events’ halfwidth duration through time for an islet exposed to a quadruple 16 mM glucose stimulation protocol (purple areas of the protocol bar at the bottom of the pane) with resting periods in 6 mM glucose (white protocol areas). Only events with z-score above 8 are presented. (C), A raster plot of [Ca2+]c events showing activity events in individual ROIs. (D), Time courses from ROIs indicated in A, and rebinned to 2 Hz (recorded at 20 Hz). The abscissa is shared for plot B–D.

Discussion

Our results show that we were able to reproduce the main characteristics of beta-cell collective response to stimuli using a simple model of coupled fast stochastic oscillators mapped onto a correlation network. Two basic elements of the model are crucial to capture the whole spectrum of beta-cell response curves: (a) decision to switch between σB states depending on the current collective state of the cell’s neighbors, and (b) ability to control the sensing precision. Both elements together determine the abruptness of the disorder-order phase transition in collective beta-cell activity. Choosing between the two waiting times to keep the network state below a certain threshold results in a very abrupt, first-order-like phase transition with the size of the giant component as an order parameter. This behavior is similar to an explosive percolation phenomenon in random networks [34], where the growth of the giant component is delayed by competing links mechanism. The phase transition of beta-cell activation seems to change from first to second order-like with gradual growth of activity, leading to the possibility that beta-cells adapt their collective behavior and move towards a critical point [4] as the stimulus approaches the threshold value. These results suggest that further experiments with a slower rate of glucose exchange are required to capture the critical point and better determine the nature of phase transitions during the beta-cell activation.

The activity of these fast stochastic oscillators in beta-cell or islet collective comes in a form of dynamics and probability distribution of Ca2+ events, which can be considered as information that fulfills all the requirements for computing. Unitary Ca2+ events are triggered randomly, and get deterministically constrained into higher order spatial and temporal patterns with functional properties of the proteins involved. The information is communicated with temporal and spatial sampling through at least two layers of fine-grained architecture to ensure robustness, enhanced sensitivity or efficiency and evolvability enabling parallel terraces scans [35] (Fig. 3). We have previously described pancreatic islets, based on the number of interconnected beta-cells within such a collective and their average physical size, as sparse collectives with enhanced sensory function, able to resolve local gradients [9]. In this way pancreas processes a certain volume of plasma at any given time, with dominant, immediate and focused responses to strong activators. At the same time a continuous and unfocused exploration of weaker, but more diverse nutrient and metabolic stimuli can be achieved, in a so-called adaptive response.

thumbnail Figure 3

Layers of fine-grained architecture in pancreas.

At this stage we can try to readdress the question, why there are so many rather small islets in the pancreas, instead of large compact gland with a few hundred million beta-cells? Interestingly, the number of islets, but not the size of the islets itself, scales with the organism′s size [36]. The distributed nature of pancreatic islets was reported to be required to locally support the function of acinar cells [37]. Alternatively, both endocrine and exocrine pancreas could be part of a sensory system, exposed to plasma levels of nutrients and metabolites, computationally solving two different tasks. Endocrine cells are primarily responsible for the metabolic economy, while acinar cells with the release of digestive enzymes which modulate the intestinal digestion and absorption. Novel data on the exact pattern of pancreas microcirculation is required to reassess whether beta-cells, as well as exocrine cells, can use local nutrient and metabolite gradients to improve their computing function. Furthermore, since islets within pancreas are interconnected with neurons, another, higher level sparse collective of islets is a possibility, which could contribute to a detection of global metabolite concentration differences and in this way contribute to the real time analytical capacity of pancreas (Fig. 3). Also here, new data on the pattern of pancreas macro- and microcirculation are required. The anatomical arrangement described above renders the distributed character of endocrine pancreas as a massive computer that parallelizes its computing both on the islet level as a computational unit and at least one higher level of biological organization.

Similarly to the description of biological computation within the immune system [2], we suggest that the pancreas combines two systems to compute whether the current metabolic challenge could be managed with small adjustments or should it be treated as a more serious threat and would justify a major hormonal response. Such a major response could in turn compromise the metabolic liquidity, i.e., instant availability of glucose for a vast majority of cells in an organism with obligatory glycolytic energy production requirement. Regular intervals between the meals as well as an initial and limited metabolic load could be intercepted by IP3-receptor-dependent cytosolic Ca2+ release in the form of slow first phase oscillations [23]. However, after a big meal or a larger metabolic load, a higher burden of different nutrients could initiate a full biphasic response with initial slow component, followed by an adaptive RyR-dependent response (Figs. 2 and 4). This latter activity can manifest itself in beta-cells as a spectrum of different phenotypes [38]. The main reason for this diversity of responses is that short sub-second CICR event temporally summate into a variety of self-similar patterns of short events that last for some seconds and further into longer events of some tens of seconds (Fig. 2). This designed response is self-limited by reduced availability of Ca2+ within the ER when nutrient levels drop postprandially [39]. Oscillations of [Ca2+]c result from the activity of IP3 and ryanodine receptors, with the latter taking a more dominant role in later phases of stimulation or during stronger stimulations. Such duality of the contributions of these Ca2+ release channels has been previously suggested to provide a basis for complex patterns of intracellular Ca2+ regulation of neuronal activity [14].

thumbnail Figure 4

Timescales of the collective activity in pancreas, measured as [Ca2+]c events in a typical day. Basal oscillatory activity with the period between 5 and 10 mins throughout the day (upper band) is increased after meals in a typical biphasic manner with a first peak followed by a plateau activity. On top of the basal oscillatory activity, a faster series of few seconds long bursts develops (middle band) as a temporal summation of unitary sub second events (lower band). The fast bursts can with a higher stimulation further summate to slow events of some tens of seconds during the plateau phase. Both, IP3 and ryanodine receptors contribute to the unitary events, however the former is dominant during the initial phase and the latter during the plateau phase.

An organization as described above would have further repercussions. For example, it can form a basis for a circuit memory, which could be amplified after a repetitive stimulation or which can be rewritten by stochastic editing to yield counterfactual future goals that would first express themselves only at the onset of a major perturbation, without leaving a clear causal link to the molecular organizational level, which is an exclusive focus of all current investigations [40]. And furthermore, a long-term, constant and strong activation of the adaptive system can lead to receptor destabilization and hyperactivity that can have potentially perilous effect on the health of endocrine pancreas and metabolic economy of an organism, eventually leading to diabetes mellitus. Recent experimental data support the last claim, since inhibition of the ryanodine receptor hyperactivity restored the dysfunctional glucose-induced [Ca2+]c oscillations in the ER stress context [41].

Materials and methods

Ethics statement

We conducted the study in strict accordance with all national and European recommendations on care and handling experimental animals, and all efforts were made to minimize the suffering of animals. The Ministry of Education, Science and Research, Republic of Austria (No: 2020-0.488.800).

Tissue slice preparation and dye loading

Eight weeks old C57BL/6J male mice (Jackson Laboratories) were kept on a 12:12 hours light: dark schedule in individually ventilated cages (Allentown LLC, USA) and used to prepare pancreatic tissue slices, as described previously [23]. In brief, after sacrificing the mice with CO2 and cervical dislocation, we accessed the abdominal cavity via laparotomy and distally clamped the common bile duct at the major duodenal papilla. Proximally, we injected the low-melting-point 1.9% agarose (Lonza, USA) dissolved in extracellular solution (ECS, consisting of (in mM) 125 NaCl, 26 NaHCO3, 6 glucose, 6 lactic acid, 3 myo-inositol, 2.5 KCl, 2 Na-pyruvate, 2 CaCl2, 1.25 NaH2PO4, 1 MgCl2, 0.25 ascorbic acid) at 40 °C into the common bile duct. Immediately after injection, we cooled the agarose infused pancreas with ice-cold ECS and extracted it. We prepared tissue slices with a thickness of 140 μm with a vibratome (VT 1000 S, Leica) and collected them in HEPES-buffered ECS at RT (HEPES-buffered ECS, consisting of (in mM) 125 NaCl, 10 HEPES, 10 NaHCO3, 6 glucose, 6 lactic acid, 3 myo-inositol, 2.5 KCl, 2 Na-pyruvate, 2 CaCl2, 1.25 NaH2PO4, 1 MgCl2, 0.25 ascorbic acid; titrated to pH = 7.4 using 1 M NaOH). For staining, we incubated the slices for 50 min at RT in the dye-loading solution (6 μM Calbryte 520, AAT Bioquest), 0.03% Pluronic F-127 (w/v), and 0.12% dimethylsulphoxide (v/v) dissolved in HEPES-buffered ECS). All chemicals were obtained from Sigma-Aldrich (St. Louis, Missouri, USA) unless otherwise specified.

We transferred individual pancreatic slices to a perifusion system containing 6 mM glucose in HEPES-buffered ECS at 34 °C. Slices were exposed to a series of four square-pulse-like stimulations (quadruple protocol) characterized by exposure to 16 mM glucose for either 2 or 15 min during the last stimulation round respectively, each followed by a washout with sub-stimulatory 6 mM glucose concentration until all the activity switched off. Imaging was performed on standard inverted confocal microscope equipped with resonant scanners (Leica Microsystems TCS SP8) with 20× high NA objective lens. Acquisition frequency was set to 20 Hz at 256 × 256 pixels, with pixels size close to 1 μm2 to allow for a precise quantification of [Ca2+]c oscillations. Calbryte 520 was excited by a 490 nm line of a white laser. The emitted fluorescence was detected by HyD hybrid detector in the range of 500–700 nm using a photon counting mode.

Analysis and processing of data

The analysis of [Ca2+]c events has been performed as previously described [23]. Briefly, the movies were processed using custom Python script to automatically detect ROIs corresponding to individual cells. Within the detected ROIs the events were characterized by the start time, peak point time at the maximal amplitude, and the width of the pulse at the half of the height, which is a parameter we used to evaluate the duration of the event. The processing step included motion and phase correction. Beta-cells were identified based on their typical activity pattern, being inactive at non-stimulatory glucose concentration (6 mM) and activating when stimulated by 16 mM glucose. All cells outside histologically identifiable islet have been discarded from further analysis. In the next step, [Ca2+]c events were automatically distilled and annotated from each ROI.

Conflict of interest

The authors declare no conflict of interest, financial or otherwise.

Acknowledgments

MSR received financial support from NIH (R01DK127236) and from the Austrian Science Fund/Fonds zur Förderung der Wissenschaftlichen Forschung (bilateral grants I3562-B27 and I4319-B30). AS, DK and MSR received financial support from the Slovenian Research Agency (research core funding program no. P3-0396 and projects no. N3-0048, no. N3-0133 and no. N3-9289). DK was further supported from the Slovenian Research Agency project no. J7-3156. Presented in part at the Theodor Billroth’s Lecture, Wed, Dec 14, 2022, online webinar.

Author contributions

All authors contributed substantially to all aspects of the study. Professor Dr. Marjan Slak Rupnik is 4open Senior Editorial Board member.

References

  1. Schnitzer MJ (2002), Biological computation: amazing algorithms. Nature 416, 683. [Google Scholar]
  2. Mitchell M (2009), Complexity: a guided tour, Oxford University Press. [Google Scholar]
  3. Tkacik G, Bialek W (2016), Information processing in living systems. Annu Rev Condens Matter Phys 7, 12. [Google Scholar]
  4. Mora T, Bialek W (2011), Are biological systems poised at criticality?, J Stat Phys 144, 268. [Google Scholar]
  5. Langton CG (1990), Computation at the edge of chaos: phase transitions and emergent computation, Phys D: Nonlinear Phenom 42, 12. [Google Scholar]
  6. Cahill GF (1970), Starvation in man, N Engl J Med 282, 668. pMID: 4915800 [Google Scholar]
  7. Haas A, Borsook D, Adler G, Freeman R (2022), Stress, hypoglycemia, and the autonomic nervous system, Auton Neurosci 240, 102983. [CrossRef] [PubMed] [Google Scholar]
  8. Levin M, Dennett DC (2020), Cognition all the way down – Biology’s next great horizon is to understand cells, tissues and organisms as agents with agendas (even if unthinking ones). https://aeon.co/essays/how-to-understand-cells-tissues-and-organisms-as-agents-with-agendas. [Google Scholar]
  9. Korošak D, Slak Rupnik M (2018), Collective sensing of β-cells generates the metabolic code, Front Physiol 9, 31. https://doi.org/10.3389/fphys.2018.00031. [PubMed] [Google Scholar]
  10. Noble D (2012), A theory of biological relativity: no privileged level of causation, Interface Focus 2, 55. [CrossRef] [PubMed] [Google Scholar]
  11. Cerasi E, Luft R (1967), The plasma insulin response to glucose infusion in healthy subjects and in diabetes mellitus, Eur J Endocrinol 55, 278. [CrossRef] [Google Scholar]
  12. Curry DL, Bennett LL, Grodsky GM (1968), Dynamics of insulin secretion by the perfused rat pancreas, Endocrinology 83, 572. [CrossRef] [PubMed] [Google Scholar]
  13. Berglund O (1980), Different dynamics of insulin secretion in the perfused pancreas of mouse and rat, Eur J Endocrinol 93, 54. [CrossRef] [Google Scholar]
  14. Watras J, Ehrlich BE, et al. (1991), Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum, Nature 351, 751. [Google Scholar]
  15. Wollheim CB, Kikuchi M, Renold AE, Sharp GW, et al. (1978), The roles of intracellular and extracellular Ca++ in glucose-stimulated biphasic insulin release by rat islets, J Clin Investig 62, 451. [CrossRef] [PubMed] [Google Scholar]
  16. Grodsky GM, et al. (1972), A threshold distribution hypothesis for packet storage of insulin and its mathematical modeling, J Clin Investig 51, 2047. [CrossRef] [PubMed] [Google Scholar]
  17. Rorsman P, Renström E (2003), Insulin granule dynamics in pancreatic beta cells, Diabetologia 46, 1029. [CrossRef] [PubMed] [Google Scholar]
  18. Straub SG, Sharp GW (2004), Hypothesis: one rate-limiting step controls the magnitude of both phases of glucose-stimulated insulin secretion, Am J Physiol Cell Physiol 287, C565. [CrossRef] [PubMed] [Google Scholar]
  19. Watts M, Fendler B, Merrins MJ, Satin LS, Bertram R, Sherman A (2014), Calcium and metabolic oscillations in pancreatic islets: who’s driving the bus?, SIAM J Appl Dyn Syst 13, 683. [Google Scholar]
  20. Nesher R, Cerasi E (1987), Biphasic insulin release as the expression of combined inhibitory and potentiating effects of glucose, Endocrinology 121, 1017. [CrossRef] [PubMed] [Google Scholar]
  21. Stozer A, Skelin Klemen M, Gosak M, Krizančić Bombek L, Pohorec V, Slak Rupnik M, Dolensek J (2021), Glucose-dependent activation, activity, and deactivation of beta cell networks in acute mouse pancreas tissue slices, Am J Physiol Endocrinol Metab 321, E305. [CrossRef] [PubMed] [Google Scholar]
  22. Sluga N, Postić S, Sarikas S, Huang Y-C, Stozer A, Slak Rupnik M (2021), Dual mode of action of acetylcholine on cytosolic calcium oscillations in pancreatic beta and acinar cells in situ, Cells 10, 1580. [CrossRef] [PubMed] [Google Scholar]
  23. Postić S, Sarikas S, Pfabe J, Pohorec V, Krizančić Bombek L, Sluga N, Skelin Klemen M, Dolenšek J, Korošak D, Stozer A, Evans-Molina C, Johnson JD, Slak Rupnik M (2022), High-resolution analysis of the cytosolic Ca2+ events in β cell collectives in situ, Am J Physiol Endocrinol Metab, E42–E55. https://doi.org/10.1152/ajpendo.00165.2022. [PubMed] [Google Scholar]
  24. Sluga N, Krizančić Bombek L, Kerčmar J, Sarikas S, Postić S, Pfabe J, Skelin Klemen M, Korošak D, Stozer A, Slak Rupnik M (2022), Physiological levels of adrenaline fail to stop pancreatic beta cell activity at unphysiologically high glucose levels, Front Endocrinol 13. https://doi.org/10.3389/fendo.2022.1013697. [CrossRef] [Google Scholar]
  25. Berridge MJ, Bootman MD, Lipp P (1998), Calcium – a life and death signal, Nature 395, 645. [Google Scholar]
  26. Berridge MJ, Lipp P, Bootman MD (2000), The versatility and universality of calcium signalling , Nat Rev Mol Cell Biol 1, 11. [Google Scholar]
  27. Bootman MD, Bultynck G (2020), Fundamentals of cellular calcium signaling: a primer, Cold Spring Harb Perspect Biol 12, a038802. [CrossRef] [PubMed] [Google Scholar]
  28. Nikitin A, Néda Z, Vicsek T (2001), Collective dynamics of two-mode stochastic oscillators, Phys Rev Lett 87, 024101. [Google Scholar]
  29. Podobnik B, Korošak D, Klemen MS, Stozer A, Dolenšek J, Rupnik MS, Ivanov PC, Holme P, Jusup M (2020), β cells operate collectively to help maintain glucose homeostasis, Biophys J 118, 2588. [CrossRef] [PubMed] [Google Scholar]
  30. Korošak D, Jusup M, Podobnik B, Stozer A, Dolenšek J, Holme P, Rupnik MS (2021), Autopoietic influence hierarchies in pancreatic cells, Phys Rev Lett 127, 168101. [Google Scholar]
  31. Fancher S, Mugler A (2017), Fundamental limits to collective concentration sensing in cell populations, Phys Rev Lett 118, 078101. [Google Scholar]
  32. Beauvois MC, Merezak C, Jonas J-C, Ravier MA, Henquin J-C, Gilon P (2006), Glucose-induced mixed [Ca2+]c oscillations in mouse beta-cells are controlled by the membrane potential and the SERCA3 Ca2+-ATPase of the endoplasmic reticulum, Am J Physiol Cell Physiol 290, C1503. [CrossRef] [PubMed] [Google Scholar]
  33. Gosak M, Stozer A, Markovic R, Dolensek J, Perc M, Slak Rupnik M, Marhl M (2017), Critical and supercritical spatiotemporal calcium dynamics in beta cells, Front Physiol 8. https://doi.org/10.3389/fphys.2017.01106. [CrossRef] [Google Scholar]
  34. Achlioptas D, D’Souza RM, Spencer J (2009), Explosive percolation in random networks, Science 323, 1453. [Google Scholar]
  35. Rehling J, Hofstadter D (1997), in 1997 IEEE International Conference on Intelligent Processing Systems (Cat. No.97TH8335), 28–31 October 1997, Beijing, China, vol. 1, pp. 900–904. https://doi.org/10.1109/ICIPS.1997.672938. [Google Scholar]
  36. Jo J, Choi MY, Koh D-S (2007), Size distribution of mouse Langerhans islets, Biophys J 93, 2655. [CrossRef] [PubMed] [Google Scholar]
  37. Henderson J (1969), Why are the islets of Langerhans, Lancet 294, 469. [Google Scholar]
  38. Manning Fox JE, Gyulkhandanyan AV, Satin LS, Wheeler MB (2006), Oscillatory membrane potential response to glucose in islet beta-cells: a comparison of islet-cell electrical activity in mouse and rat, Endocrinology 147, 4655. [CrossRef] [PubMed] [Google Scholar]
  39. Klec C, Madreiter-Sokolowski CT, Stryeck S, Sachdev V, Duta-Mare M, Gottschalk B, Depaoli MR, Rost R, Hay J, Waldeck-Weiermair M, Kratky D, Madl T, Malli R, Graier WF (2019), Glycogen synthase kinase 3 beta controls presenilin-1-mediated endoplasmic reticulum Ca2+ leak directed to mitochondria in pancreatic islets and β-cells, Cell Physiol Biochem 52, 57. [CrossRef] [PubMed] [Google Scholar]
  40. Durant F, Morokuma J, Fields C, Williams K, Adams DS, Levin M (2017), Long-term, stochastic editing of regenerative anatomy via targeting endogenous bioelectric gradients, Biophys J 112, 2231. [CrossRef] [PubMed] [Google Scholar]
  41. Yamamoto WR, Bone RN, Sohn P, Syed F, Reissaus CA, Mosley AL, Wijeratne AB, True JD, Tong X, Kono T, Evans-Molina C (2019), Endoplasmic reticulum stress alters ryanodine receptor function in the murine pancreatic β cell, J Biol Chem 294, 168. [CrossRef] [PubMed] [Google Scholar]

Cite this article as: Korošak D, Postić S, Stožer A & Slak Rupnik M 2023. Collective biological computation in metabolic economy. 4open, 6, 3.

All Figures

thumbnail Figure 1

Empirical data showing glucose-dependent beta-cell activation and coupled stochastic oscillators model results. Glucose-dependent activity (A), from left to right: 16 mM, 12 mM, and 7 mM, data from [21], size of giant component of correlation networks (B). Parameters used in model calculations: random regular network with N = 102 and k = 10, T = 105, . Noise Σ = 0, 0.1, 3, 7. Threshold value for correlation networks was set to c0 = 0.1.
In the text
thumbnail Figure 2

Response adaptivity and memory. (A) Regions of interest (ROIs) obtained by our segmentation algorithm [23]. The color indicates the number of events identified in the ROI trace, upon a high-pass filtering at 0.2 Hz. We discarded ROIs with number of events below the threshold (red dashed line in the histogram in the lower panel). Indicated are the ROI numbers whose filtered traces correlate best with the average trace for the whole islet. The most active cells indicated with blue tones present beta-cell in the core of the islet. (B) Events’ halfwidth duration through time for an islet exposed to a quadruple 16 mM glucose stimulation protocol (purple areas of the protocol bar at the bottom of the pane) with resting periods in 6 mM glucose (white protocol areas). Only events with z-score above 8 are presented. (C), A raster plot of [Ca2+]c events showing activity events in individual ROIs. (D), Time courses from ROIs indicated in A, and rebinned to 2 Hz (recorded at 20 Hz). The abscissa is shared for plot B–D.
In the text
thumbnail Figure 3

Layers of fine-grained architecture in pancreas.
In the text
thumbnail Figure 4

Timescales of the collective activity in pancreas, measured as [Ca2+]c events in a typical day. Basal oscillatory activity with the period between 5 and 10 mins throughout the day (upper band) is increased after meals in a typical biphasic manner with a first peak followed by a plateau activity. On top of the basal oscillatory activity, a faster series of few seconds long bursts develops (middle band) as a temporal summation of unitary sub second events (lower band). The fast bursts can with a higher stimulation further summate to slow events of some tens of seconds during the plateau phase. Both, IP3 and ryanodine receptors contribute to the unitary events, however the former is dominant during the initial phase and the latter during the plateau phase.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.